我们今天来聊聊数字信号处理的基础知识:信号量化问题。
量化是将模拟信号转换为数字信号(另一个过程是采样,如文章《数字信号处理基础:什么是采样?》)时所发生的两种过程之一。当信号被量化时,ADC在每个采样时刻所取的幅度值被映射到一组离散可能的幅度水平中的一个。因此,在采样和量化过程的输出端,模拟信号在时间和幅度上都被离散化——换句话说,它已被转换为数字信号。
1.量化过程
为了更详细地定义量化过程,我们假定ADC具有一定的分辨率位数N,因此可以表示2^N不同的值。这些值对应于输入信号样本所映射到的离散量化级集。通常采用如图1所示的线性方式进行量化,尽管一个实际的ADC会有比这个例子多得多的位数(量化电平)。
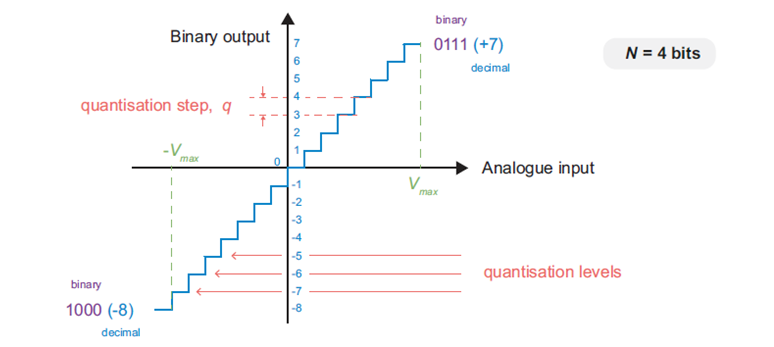
N的值越大,在ADC的工作范围内分布的量化电平的数量就越大。我们注意到一个轻微的不平衡(负量化电平比正量化电平多一个),但是对于N的实际值,这种影响可以忽略不计。当模拟样本被量化时,它们被“移动”到最接近的可用量化水平;当值较大时,转换更准确,即分辨率更高。更正式地说,模拟和量化样本之间的振幅变化被称为量化误差。其中是ADC的最大输入电压,量化步长(或间隔),表示为
位转换器的动态范围是一种常用的性能值,表示最大与最小可表示数的比值,通常用dB表示。它被定义为
因此,12位转换器的动态范围约为6×12=72dB 。一个正弦波量化的例子如图2所示,使用两种不同的量化器:首先使用4位精度,然后使用6位精度。参考(未量化采样)和量化正弦波在这里以大格式再现,以便于检查-量化引入的误差在4位情况下相对明显,但当使用6位量化时,它们更难看到。因此,我们可以说,用6位分辨率量化信号比4位等效信号产生更小的幅度误差。虽然量化产生的误差很难在时域观察到,但在6位时,在频域观察时,这仍然代表着信号质量的相当大的退化。用于大多数应用的实际ADC和DAC至少使用8位精度。目前,Xilinx所有RFSoC器件至少具有12位ADC(第1代和第2代器件具有12位ADC,第3代具有14位ADC);都有14位DAC。
常用的AD9361具有12bit位宽数字接口,9026具有14bit的DAC和16bit的ADC。

2.量化误差
当考虑单个样本的量化,并将其振幅移动到最接近的量化水平时,可以得出最坏情况误差是一个量化区间的一半。用符号表示量化区间的幅度,因此最大误差为。假设输入量化器的样本幅值是随机的,则可以形成如图3所示的概率密度函数(Probability Density Function, PDF)。该PDF的面积为1,这意味着当对特定样本进行量化时,一定会出现到范围内的量化误差。
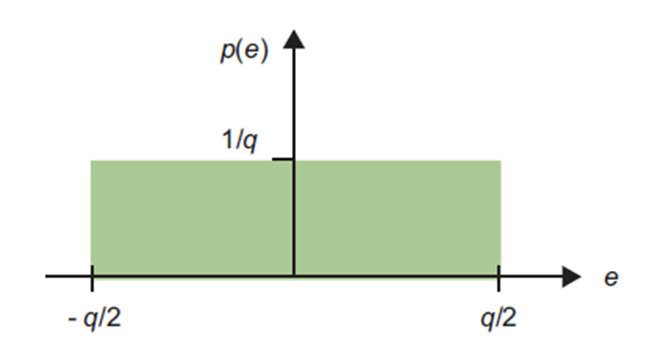
因此,可以根据量化误差的统计期望来分析与ADC相关的量化噪声。正如我们稍后将看到的,误差在整个范围内是等概率的假设并不总是成立,因为误差的分布取决于被量化的信号的性质。然而,图3的PDF提供了一种有用的机制来定量分析量化过程中引入的噪声。现在我们将继续考虑量化噪声是如何产生和被量化的。
3.量化噪声
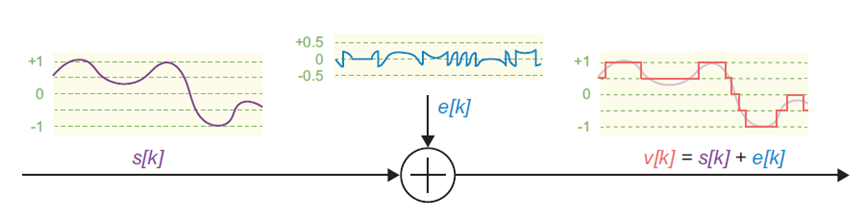
前一节讨论的量化过程也可以建模为加入了噪声。每个量化样本都存在误差,量化样本索引处可表示为
其中为量化后的样本,为真实的(未量化的)样本值,为两者之差(即量化误差)。这个过程如图4所示。
量化误差信号的功率(即ADC的量化噪声功率)可以根据图4.10的误差PDF导出。误差信号的平方,由误差概率加权,在所有可能的误差值上进行积分。由于可能误差值的范围被限制在到的范围内,积分可以在这些范围内求值。
注意到,对于的所有值,误差功率表示为
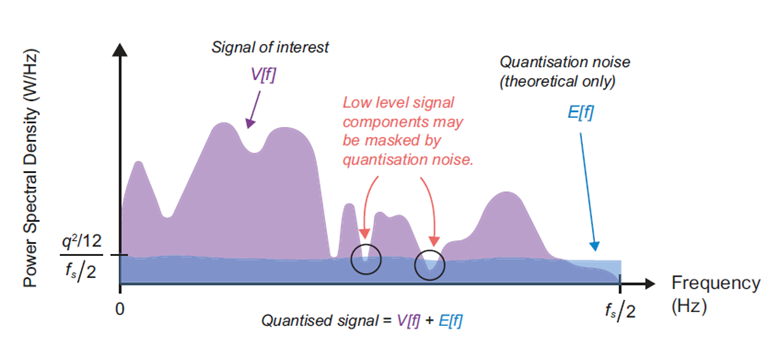
其中为量化区间。因此,我们可以确认,随着量化器位数的增加,ADC引入的噪声功率会降低(因为这会导致更小的量化间隔)。理论上,量化误差信号从0Hz延伸到的整个基带区域,因此,有可能感兴趣的信号中存在的低电平分量会被量化噪声的存在“掩盖”,如图5所示。根据我们上面的分析,这个问题对于低分辨率ADC(即那些具有很少位的ADC)来说更为严重,因此高分辨率ADC的动机是明确的。根据目前的技术,在非常高(Gsps)采样率下工作的ADC不能像低频应用(如音频处理(以数十ksps工作)的ADC那样提供那么多比特。
4. 周期信号和频率杂散
并非所有ADC量化器的输入信号都会产生上一节讨论的随机量化误差。如果输入信号是周期性的,则量化误差序列遵循重复的模式,因此量化误差信号也是周期性的。我们可能还会发现,只生成了可能的量化误差值的一个子集(与图3中的PDF相反,它假设了随机性)。正弦波的数字化就是一个很好的例子。我们可以观察到,在一段时间后,量化误差的序列重复;重复周期由采样周期和正弦波周期之间的关系来定义。由此产生的量化误差信号也是周期性的,其周期性分量对应于频域中不需要的音调(“杂散”)。
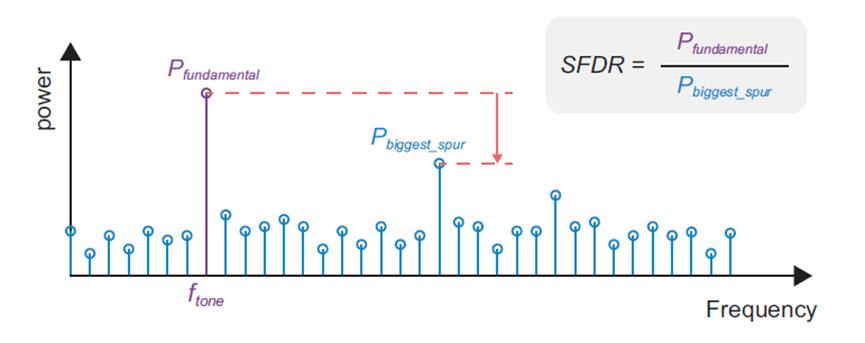
然而,在实践中,被量化的信号通常比单个正弦波更复杂(例如,在通信中,基带信号由一系列频率分量组成),因此杂散问题不太明显。频率杂散是谐波信号失真的一种形式,是不可取的。这种失真的程度是通过度量无杂散动态范围(SFDR)来量化的,SFDR是基本分量(例如正弦波)和最显著的杂散之间的比率,以dB表示。
SFDR的概念如图6所示。除了使用更高分辨率ADC(即增加位数)的最直接解决方案外,另一种常见方法是在量化之前向ADC输入添加“抖动”信号。抖动信号是低电平噪声,它引入了足够的随机性来防止量化误差的严格周期性,从而避免了频率杂散的产生。虽然增加噪声来改善信号质量似乎有悖直觉,但使用抖动可以有助于抑制杂散频率成分,从而改善SFDR。这通常是通信系统的主要关注点。