作者：Lgnited

本文由面包版社区版主原创，未经版主同意，禁止转载

https://mbb.eet-china.com/forum/topic/84559_1_1.html

【演算傅里叶变换在电路中的应用，顺便看能不能推导出对应的数学模型或者数学公式】

傅里叶变换的篇章比较多，也非常的有意思啊，大学时学没怎么明白。巧不巧的，又遇上了，因为项目需要设计一个低噪声正弦波小信号(周期性、连续性)驱动电路。

篇章1，言归。傅里叶级数是一个自然的函数展开形式，公式如下：

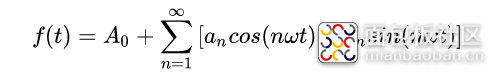
由此公式可以看出来，这是一个一个变量解后再求和的过程。在(负无穷，正无穷)间，满足“绝对可积”，是傅里叶级数变换往傅里叶积分的拓展关键性质，傅里叶积分再拓展就是就是傅里叶变换了，对应的频谱分析上，w的范围从(0，正无穷)延伸到(负无穷，正无穷)。

为了更形象在电路上展示和应用傅里叶变换才做如此实验的篇章1。演示傅里叶(逆)变化在数字滤波的实验流程。

下面一个小测试，进行一个正弦波的频谱分析。首先，正弦波是一个时域连续的周期函数，它在电路上的重要特性就是波形失真，噪声大。通常其失真就意味着波形掺杂高次谐波。

实验1)和实验2)是展示两个不同频率时域波形的频域。

实验3)是将实验1)和实验2)两个时域波形合并后的频域。

实验4)简单的数字滤波，将基波外的谐波滤波掉。

实验1)

【参数】【输入波形：10KHZ, 5V幅度，无偏置,sin】，再串联2个并联470K电阻(实验室回来拿错，没有替代电阻)。

实验1小结)时域上：时域波形和输入波形的幅度不一致(原因见电路工程数学-阻性分析模型)，但时域波形幅度不影响频谱分析。

频域上：10K频率时域波形，在10KHZ(x轴)左右凸起一个小山丘(这里波形不太平滑，可能和示波器分辨率和采样点有关)。这就是时域周期连续信号在频域这个维度上的呈现。

实验2)

【参数】【输入波形：50KHZ, 5V幅度，无偏置,sin】，再串联2个并联470K电阻，测试如下图所示

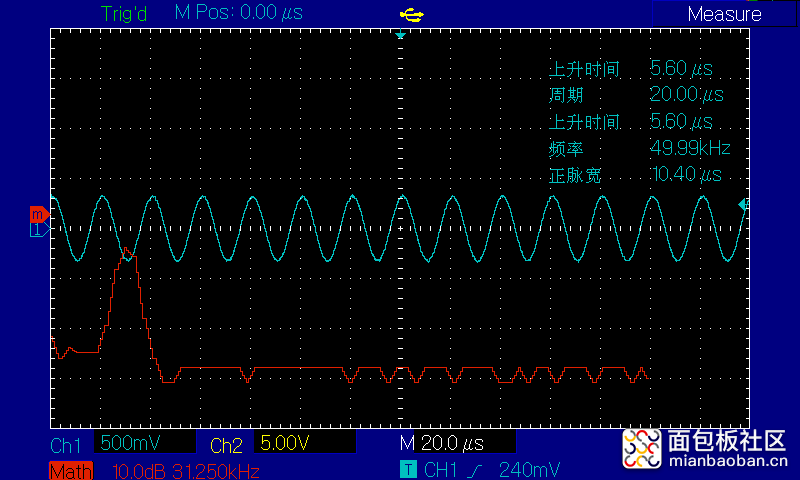
实验2小结) 频域上：50K频率时域波形，在50KHZ(x轴)左右凸起一个小山丘。频谱和对应时域波的频率相关，频率改变，频谱也会随着变化。

实验3)

【参数】【输入波形：实验1)和实验2)波形合并】，即【50kHZ和10kHZ的波形合并】，测试如下两图所示,图一是串联了一个大电阻，图二是没有串联电阻

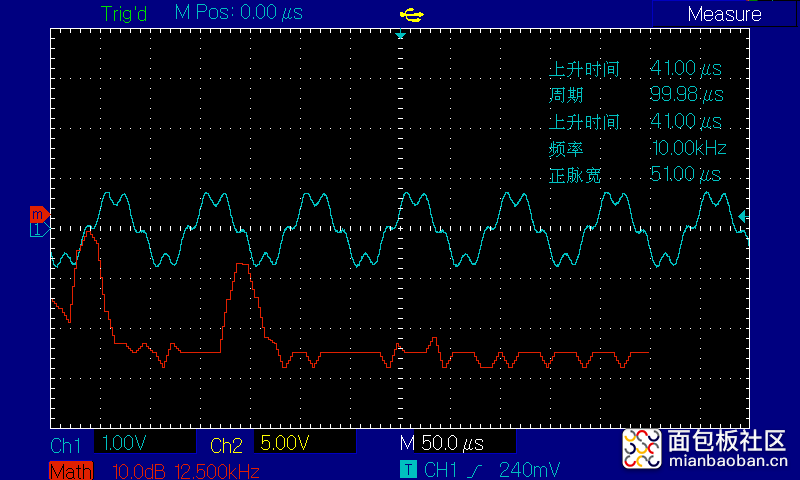
实验3小结) 时域上：高阻抗改变了输入波形，其中包括了幅度和主要形状(原因见电路工程数学-阻性分析模型)，不影响频域分析。

频域上：两个不同频率的波形，在时域上合并后，波形上可能复杂难以分辨。但在频域上可以分辨，并可以显示出频率大小和范围，这为数字滤波电路提供了数据依据。

实验4)

【参数】【输入波形：11MHZ和10KHZ 的波形合并，其他性质保持一致】

实验4小结)傅里叶可以实现滤波电路的重要依据。(这里的滤波电路还不够好，还有个250KHZ的小幅度的杂波没有滤掉，源于没有元器件搭建)

测试小结结论：

1、 频谱是滤波的关键，合适的频率点设计合适的滤波电路，可以去除不必要的波形

2、 噪声可能会影响到频谱的有效分析，反之频谱亦是排除噪声的有效途径

3、 时域合并波形，频域上可以被分离和还原，应用于音频电路设计的参考依据

4、 频谱是可以衡量一个波形失真程度

5、 时域波形的同相位上，合并幅度有一定的相加减作用(或可能与周期相关)

6、 可以用于分析多种波形合并成一种新的波形，反之亦可逐个分离的研究

7、 合并的波形，基波的频谱若不变。随着谐波次数的增加，从影响基波的整体波形的周期上，转变到影响波形的线上一小截周期，并影响随着谐波次数增加而变小。

8、 频谱有呈现出收敛性质

9、 谐波次数增加，谐波分量的振幅越小

10、时域波形进行傅里叶变换到频域，把不必要的频率分量滤除，再傅里叶逆变换到时域波形，是实验本次实验的目的。

‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧END‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧