大马拉小车的节能问题-icspec

大马拉小车的节能问题

来源:jsp 发布时间:2015-07-10

分享至微信

0 引言

时至今日，知道变频调速的人已经相当的普遍了。大多数人一提起变频调速，总是能和节能挂起钩来。近年来，尽管我国在能源开发方面进展迅速，但还是跟不上需求的增长，节能问题始终处于相当突出的位置。

变频调速之所以节能，主要在于把全速运行中浪费的电能节约了下来。尤其是闭环调速系统，如恒压供水系统等，实现了按需拖动，几乎完全消除了拖动系统在运行过程中的浪费。这是从大的方面实现了节能，但并不等于节能潜力已经挖掘干净了。事实上，在许多场合，还存在着大马拉小车的现象，在这一方面，还大有潜力。本文专就大马拉小车的节能技巧问题作一探讨。

1 大马拉小车的基本分析

当负载所需的功率远小于电动机的额定功率，或者负载折算到电动机轴上的转矩远小于电动机的额定转矩时，通常称之为大马拉小车。

1.1 大马拉小车时的反电动势

电动机定子侧的电动势平衡方程

1.2 大马拉小车时的磁通

1.3 大马拉小车时的励磁电流

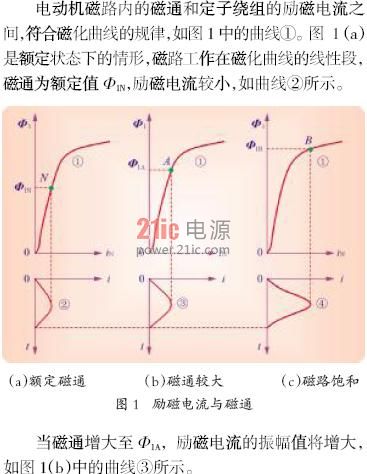
1.4 大马拉小车存在的问题

1.4.1 功率因数变差

电动机的电流平衡方程是

图2所示，是粗略的电流矢量图。图2(a)是额定状态时的情形。

轻载时，转子的折算电流小了，而励磁电流大了。结果，合成为定子电流后，和电压的相位差角增大了，而功率因数则变小了，如图2(b)所示。

1.4.2 效率降低

磁通的增加，将增大铁心的磁滞损失和涡流损失，使损耗功率的相对值增大，效率降低。

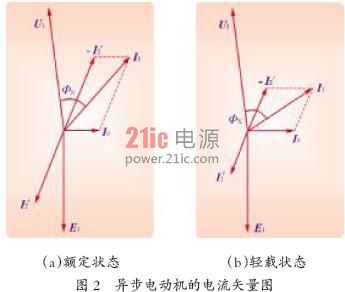
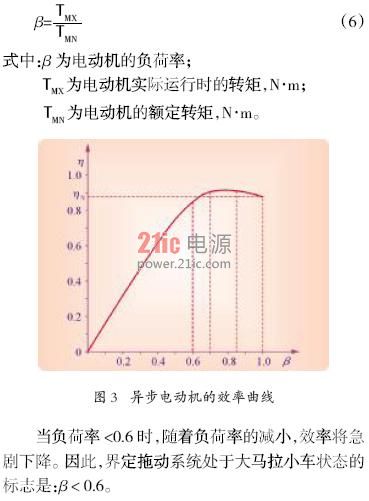
1.5 大马拉小车的界定

有关资料表明，异步电动机的最高效率发生在负荷率为0.7～0.85 的时候，其效率曲线如图3 所示，图中的横坐标是电动机的负荷率，其计算式为

2 变频器的节能技巧

由以上分析，大马拉小车的结果，首先反映在反电动势增大。显然，如果适当减小电源电压，反电动势就可以随之减小。由式(4)，磁通就可以恢复到接

近于额定值。

因此，大马拉小车节能的基本途径，便是适当降低电压。而在应用变频器的场合，节能的方法更是灵活多样。

2.1 工作频率为50 Hz时的节能方法

图4(a)所示，是大马拉小车的典型例子：当运行频率为50 Hz时，电动机的额定容量是110 kW，而负载实际所需功率只有70 kW。

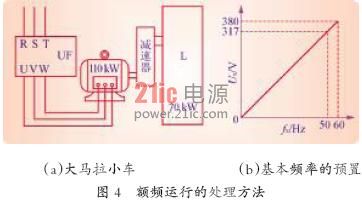
针对这种情况，降低电压的方法是加大基本频率。如图4(b)所示，如把基本频率加大为60 Hz，则60 Hz对应于额定电压380 V，而在50 Hz 时得到的电压只有317 V。

2.2 低频运行时的节能方法

二次方负载在低速运行时，极易出现大马拉小车的状态。如图5 所示，曲线①是负载的机械特性，曲线②是电动机的自然机械特性，额定转矩为TMN。在全速运行时，负载转矩等于TLN，与电动机的额定转矩十分接近。曲线③是电动机在低频运行时的机械特性，有效转矩为TEA，而负载转矩为TLD，比电动机的有效转矩小得多，所以电动机处于大马拉小车的状态。

针对上述现象，节能的基本方法如下所述。

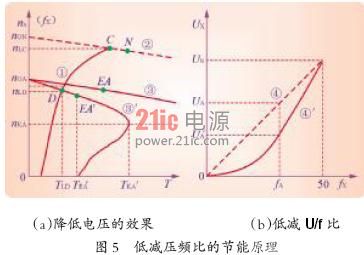
2.2.1 预置低励磁U/f比

各种变频器都设置了低励磁U/f比功能。即在低频运行时，减小U/f比，使U/f线如图5(b)中的曲线④′(曲线④为基本U/f线)所示，曲线④′通常称为低励磁U/f线。由图知，当频率为fA时，电压从UA下降为UA′。这时，电动机的磁通比额定磁通还要小，从而降低了有效转矩，使之更接近于负载转矩。

降低电压后的机械特性如图5 (a)中的曲线③′所示，电动机的有效转矩减小为TEA′，和负载转矩TLD之间的差距减小了，从而缓解了“大马拉小车”的问题。

2.2.2 自动搜索最佳工作点

变频器可以任意预置U/f比的特点，相当于在某一频率下，可以任意改变其工作电压。在任意改变其工作电压时，电流的变化规律就是电动机的电流-电压曲线，如图6 所示。

当电压偏低时，虽然磁通减小，但是励磁电流却变化不大;

另一方面，因为电动机电磁转矩的大小取决于转子电流和磁通的乘积，即

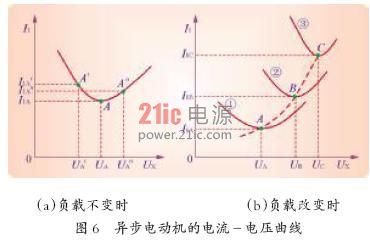
反之，当电压偏高时，一方面，由于磁通的增大，转子电流略有减小;另一方面，电动机的磁路趋向饱和，结果是励磁电流大幅度增加，在合成为定子电流

时，也使定子电流增加，如图6(a)中的A″点所示。

综合上述，得到完整的电流- 电压曲线如图6(a)所示。图中的A 点称为最佳工作点。

当负载增大时，电动机的电流和所需电压都将增大，最佳工作点向右上方移动，电流- 电压曲线也将随之移动，如图6(b)中的曲线②和曲线③所示。相应的最佳工作点如B 点和C 点所示。

某些变频器具有自动搜索最佳工作点的功能，可以在任何状态下，使运行电流为最小值，从而得到比较理想的节能效果。

3 隐形的大马拉小车现象

3.1 上限频率太低

有的用户主要利用变频器来降速，上限频率往往预置得很低。这实际上也是一种大马拉小车。

因为当上限频率低于基本频率时，电动机的有效输出功率是要减小的。

图7所示，是一个上限频率只有30 Hz 的实例。

电动机的额定容量为75 kW，但当运行在30 Hz时，其有效功率为

3.2 机械调速带恒转矩负载

机械调速大多采用齿轮箱，也有机械的无级调速器。由于驱动电动机的功率是恒定的，根据能量守恒的原理，调速器输出轴的功率也是恒定的。所以，机械调速器输出轴的机械特性具有恒功率特点，即高速时转矩小、低速时转矩大，如图8(b)中的曲线②所示。

如果用机械调速器来拖动恒转矩负载，负载的机械特性如图8(b)中的曲线①所示。[!--empirenews.page--]

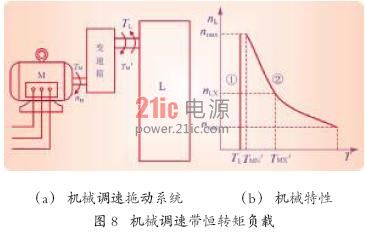
十分明显的是，为了在最高转速时也能带动负载，电动机的额定转矩必须大于负载转矩。而在额定转速以下运行时，电动机将始终处于大马拉小车的状态，如图8(b)所示。

4 恒功率负载的拖动系统

4.1 卷绕机械

以某卷绕机为例：

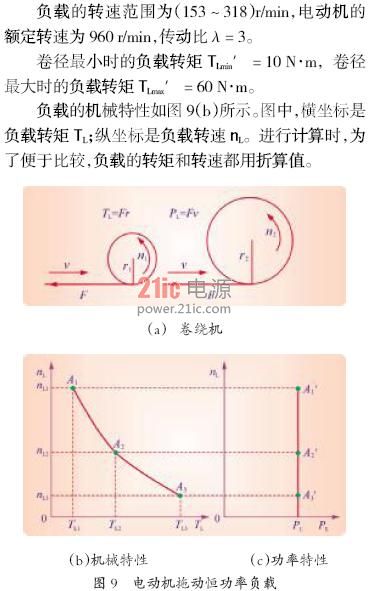
4.1.1 负载侧的计算

就是说，在卷绕的全过程中，负载的功率是恒定的，都约等于1 kW，如图9(c)所示。

4.1.2 电动机侧的计算

电动机的额定转矩必须能够带动卷径最大时的负载转矩，故有

电动机的额定转速必须满足负载的最高转速，故有

4.1.3 解决大马拉小车的途径

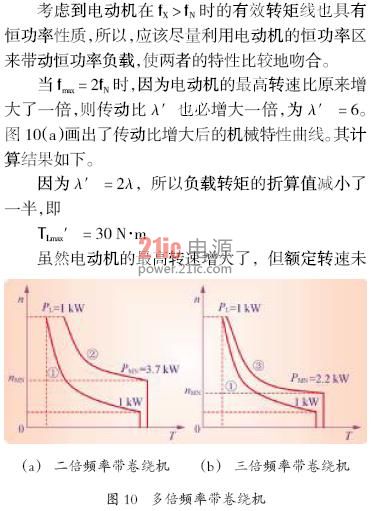
可见，所需电动机的容量减小了一半。

如果最高频率达到额定频率的3 倍，则可进一步将电动机的容量减小为2.2 kW，如图10(b)所示。

电动机如果长时间在过高频率下工作，会引起轴承磨损及动平衡等方面的问题，一般不推荐在2倍频率以上运行。但卷绕机械在最高频率下运行的时间极短，随着半径的迅速增大，卷辊的转速将迅速下降。所以，上述方案是可行的。

4.2 金属切削机床

大部分金属切削机床都属于恒转矩和恒功率混合的负载，其要点如下。

4.2.1 机械特性

以普通车床为例，负载的阻转矩如图11 中虚线框内所示，等于切削力和工件半径的乘积

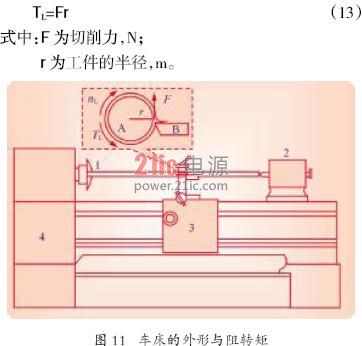
在切削深度和进刀速度不变的情况下，切削力F主要与切削的线速度成正比。因此，工件的转速越高，负载的阻转矩也越大。

但实际上，由于受到刀具和机床床身强度的限制，要求在大部分调速范围内，切削功率保持恒定。

因此，其机械特性具有恒功率的性质。

但在低速段，则因为切削力F要受到限制，故其机械特性具有恒转矩的特点。所以，金属切削机床的机械特性属于恒转矩和恒功率相混合的特性，如图12所示。

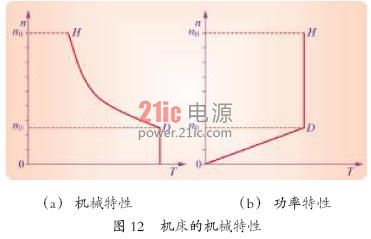
4.2.2 计算转速

恒转矩区和恒功率区的分界转速，称为计算转速，用nD表示。

关于计算转速nD大小的规定因机床的种类而不同，如在老系列车床中，一般规定：从最低速起，以全部转速挡数的1/3的最高速作为计算转速。例如，CA6140型普通车床主轴的转速共分24挡：n1、n2、n3、……n24，则第八挡转速(n8)为计算转速。

但随着刀具强度和切削技术的提高，计算转速已经大为提高。近年来，在一些新系列车床中，已逐渐提高为以最高转速的(1/4～1/2)作为计算转速

4.2.3 调速特点与减容方法

金属切削机床的转速调节，通常是在停机情况下进行的，在切削过程中，一般不进行转速调节。这是一个很重要的特点，应该充分利用。

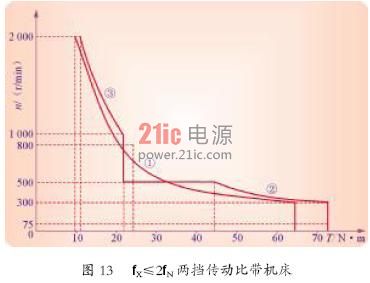
根据金属切削机床停机调速的特点，传动比可以考虑分成两挡或多挡，使变频调速后的有效转矩线尽量逼近负载的机械特性曲线。以某车床为例，如图13 所示，为了便于观察，各轴上的转矩和转速都折算到负载轴上。图13 中，曲线①是车床的机械特性;曲线②是低速段变频调速后的有效转矩线;曲线③是高速段变频调速后的有效转矩线。由图可知，电动机的有效转矩线与负载的机械特性曲线十分接近。这样做的目的，是可以使拖动系统的容量尽量地接近负载实际所需的容量.