最近再次温故线性度的相关基本概念,收益匪浅,同时对失真进行深入的研究和学习,分享下心得。本文主要介绍下线性度的基本概念,包括1dB压缩点,IP3,OP3。
电路存在非线性是个普遍现象,通常用1dB压缩点和三阶交调点来描述电路的非线性。可以用泰勒级数展开来表达电路的输入输出特性:
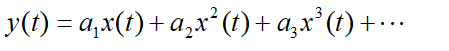
其中a1作为电路的小信号增益,a2和a3是高阶非线性系数,当输入一个正弦信号x(t)=Acos(wt) ,带入上式,忽略三次以上的非线性,得到:
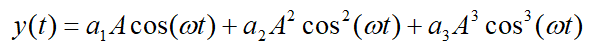
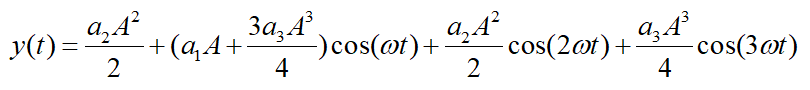
其中第一项是直流分量,直流分量是由偶次谐波产生的,如果是全差分电路,那么偶次谐波将被消除,直流分量也就消除了,但是当电路存在失配时仍会导致有限的偶次谐波。第二项为基波分量,是想要的分量;后二项分别是二次谐波和三次谐波,谐波分量的幅值和输入信号幅值A的关系分别是平方关系和三次方关系。当电路存在选频网络时,高次谐波分量被滤除,通过隔直电容或者全差分电路时消除直流分量后,只剩下基波分量,如果不存在着非线性,即a2=a3=0, 那么理想的线性系统的输出为y(t)=a1Acos(wt),而非线性导致输出为:
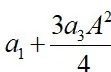
输入输出响应偏离线性关系,对于射频电路,通常a1*a3<0,因此增益受到压缩,当增益偏离线性增益1dB时,对应的输入信号幅值为输入1dB压缩点![]() ,对应的输出信号幅值为输出1dB压缩点
,对应的输出信号幅值为输出1dB压缩点![]() ,输入输出幅值也可以用功率值替代,表示为
,输入输出幅值也可以用功率值替代,表示为![]() 。如图所示表示1dB压缩点,计算输入1dB压缩点,即增益降低1dB的输入幅度值:
。如图所示表示1dB压缩点,计算输入1dB压缩点,即增益降低1dB的输入幅度值:
![]()
![]()
![]()
经化简产生的基波频率分量为:
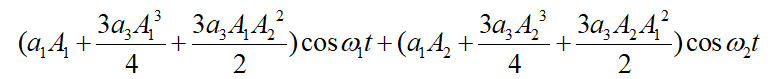
二阶交调![]() 分量为:
分量为:
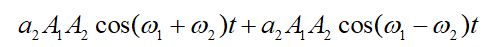
三阶交调![]() 分量为:
分量为:
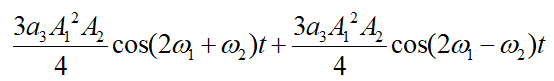
三阶交调![]() 分量为:
分量为:

令二个输入频率的幅度相同,即 A1=A2=A ,且假设A是个比较小的值,可简化基波分量为![]() ,把二阶交调归一化到基波分量上,得到 :
,把二阶交调归一化到基波分量上,得到 :
![]()
把三阶交调归一化到基波分量(三阶交调的高频分量不考虑),得到 :
![]()
在差分系统中,二阶非线性被抵消了,因此,更加关注三阶交调点,当基波幅度和三阶交调幅度相等时,即令 IM3 =1 ,得到输出三阶交调点 :
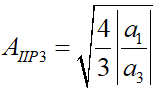
对应的输出表示为输出三阶交调![]() ,如图所示表示三阶交调点,比较输入1dB压缩点和输入三阶交调点,得到:
,如图所示表示三阶交调点,比较输入1dB压缩点和输入三阶交调点,得到:
![]()
![]()
利用MOS晶体管构成的差分对时,忽略电路失调失配的影响,有下面结论:
![]()
提高差分对MOS管的过驱动电压有利于提高线性度。当多个子系统级联时,可以推导出以下结论:
![]()
其中![]() 表示整体系统的输入三阶交调点,
表示整体系统的输入三阶交调点,![]() 表示第n级子系统的增益,
表示第n级子系统的增益,![]() 表示第n级子系统的三阶交调点。如果级联的每一级的增益都大于1,那么后级对整体系统的影响更大,直观的理解是信号每经过一级,都被放大,因此产生的非线性更加严重。
表示第n级子系统的三阶交调点。如果级联的每一级的增益都大于1,那么后级对整体系统的影响更大,直观的理解是信号每经过一级,都被放大,因此产生的非线性更加严重。
好了,总结完毕。

