在Weyl半金属中建造nonlinear Hall大厦-icspec

在Weyl半金属中建造nonlinear Hall大厦

来源:中科院半导体所发布时间:2023-01-02

分享至微信

来源：量子材料QuantumMaterials

作者：Ising

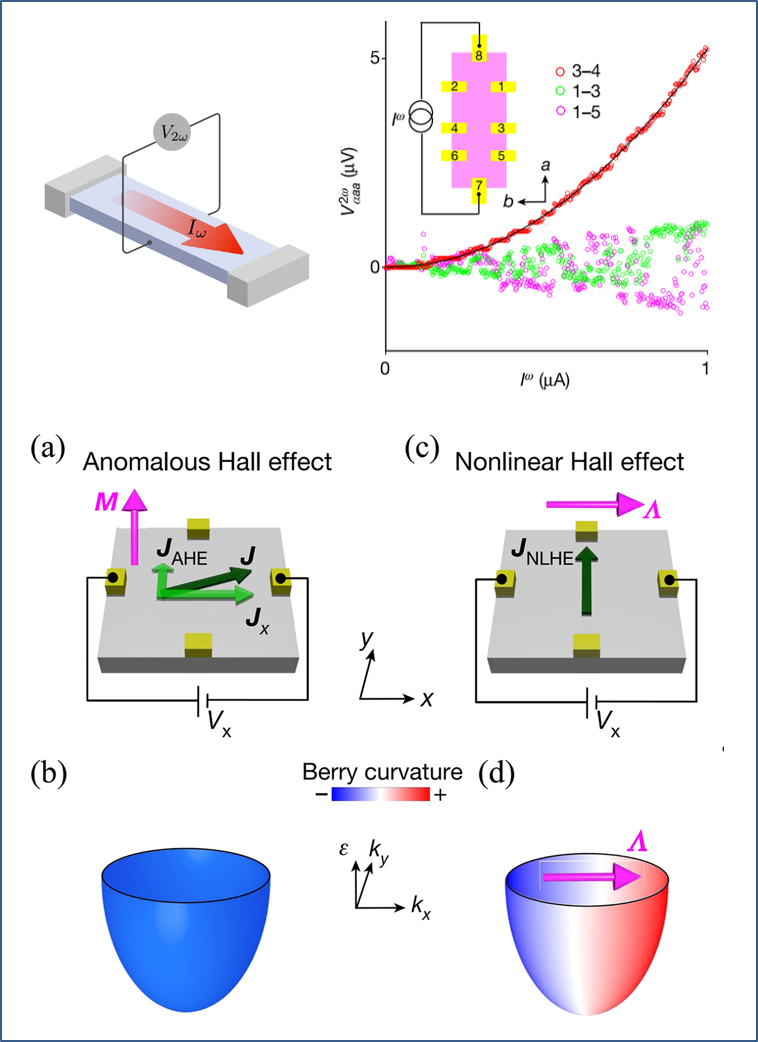
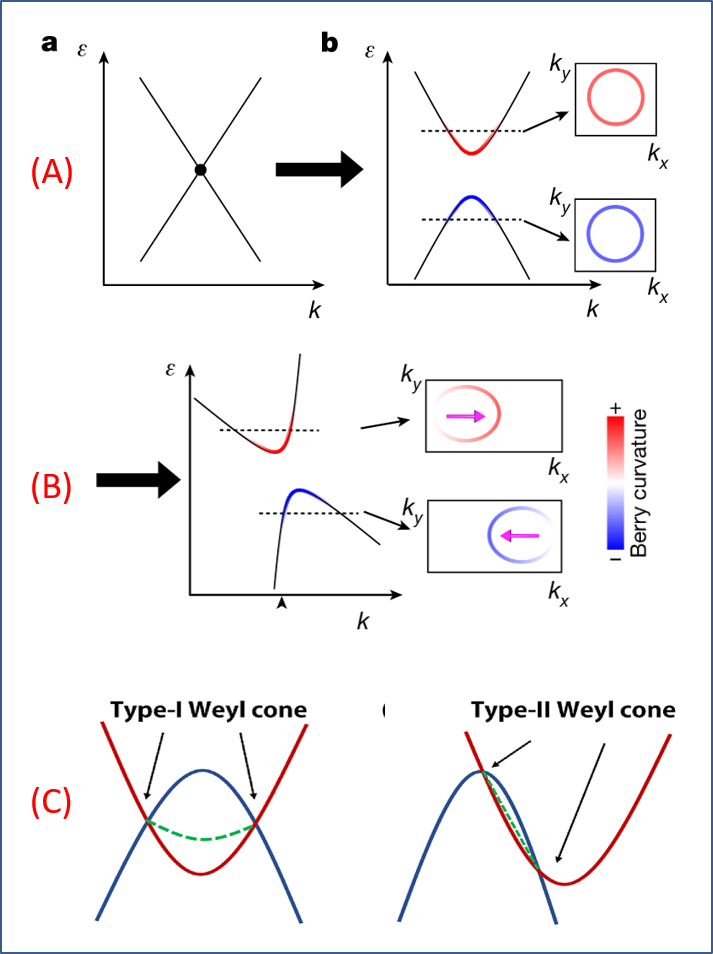
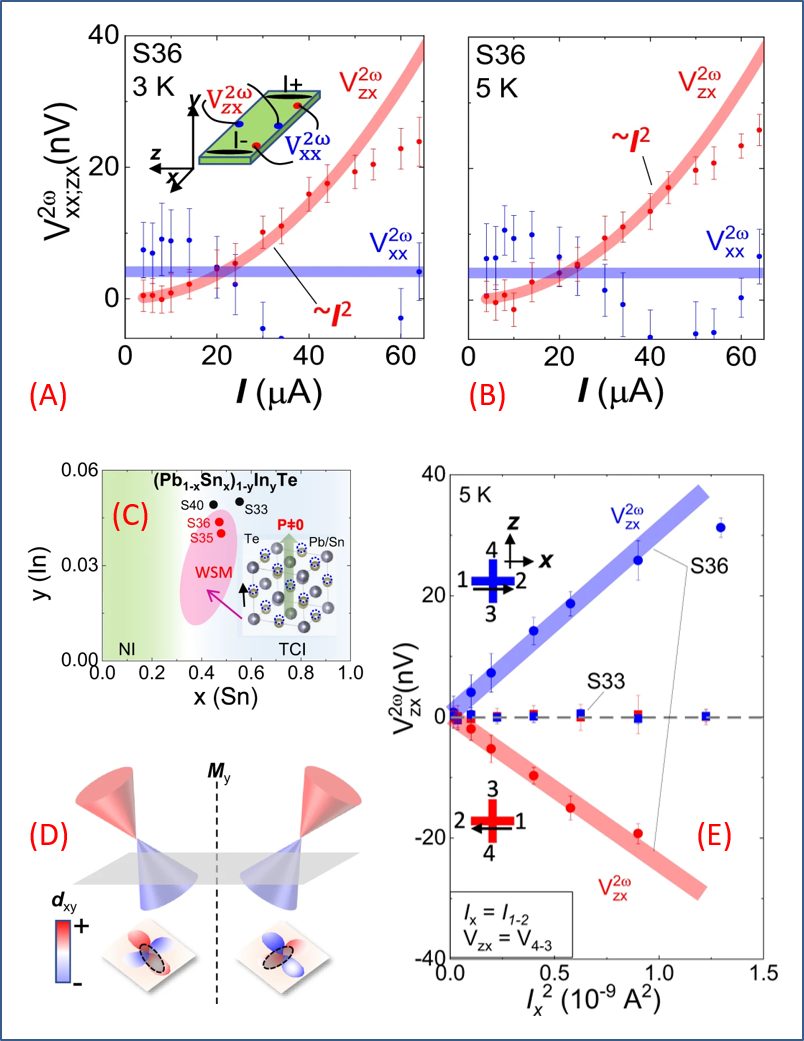
物理人认真接触和学习霍尔效应 (Hall effect)，无一例外都开始于经典电磁学中电荷于磁场引入洛伦兹力作用下的运动。洛伦兹力，与静电力一个最大的不同点，乃在于它是横向力，驱动带电载流子横向运动，并在与纵向电流和面外磁场均垂直的横向方向上产生电荷聚集、形成霍尔电压 (效应)。对非磁性体系，霍尔效应与磁场成正比。而对铁磁体系，则出现了与净磁矩成平方关系的反常霍尔效应。由此，可以利用这些性质付诸应用，例如霍尔磁强计和半导体基本性质测量 (载流子浓度与迁移率) 等。整体而言，霍尔效应更多是被用来表征物理内在规律的因变量 (结果)，很少被当成一项可资利用的性能。这一状况并不难理解，因为从洛伦兹力的大小和对应的能标来估算，要期待霍尔效应能够成为诸如电磁感应或气体热机那般肩负能量转换之机，物理人大概很少去想过。

当然，到了量子材料时代，霍尔效应的量子本源在拓扑量子的风花雪月中不断显现，终于让量子材料领域之外的物理人体会到：一个“小小的”霍尔效应，原来可以干大事、行大力。例如，霍尔效应的量子化平台，不仅仅是填充朗道能级所致，并由此成为电学基本度衡量，更多的是展示了费米面附近能带的独特拓扑几何特征。也因此，霍尔效应，从数十年前的一个简单横向电压信号，变成了今天量子物质科学舞台中央的主角之一。物理效应中那“一人得道、全家光鲜”的风气也开始弥漫开来：那些平常很少露面的霍尔家族成员 (元素)，都开始登台表演起来。

小编孤陋寡闻，以为至少有两个成员是演出了味道的：

(1) 量子反常霍尔效应：这一效应在理论概念上未必很新鲜，但一直未得实验发现。它在磁性拓扑绝缘体中得到证实，当然是量子凝聚态的大事。背后的应用潜力，还在于磁性拓扑绝缘体与当前的自旋电子学应用有可能联系起来。此道的探索，一直体现在过去十多年的拓扑量子材料发展轨迹中，在此不论。

(2) 非线性霍尔效应：这是一位新出道的角色，至少对很多凝聚态同行而言是如此。这个“非线性”之名，取得有些 misleading。最熟悉输运物理的凝聚态物理人，在此联想猜测了半天，歧义不菲，最后才和非线性光学中的那个“非线性”倍频输出联系起来。从实验现象上，这一效应，是指体系在纵向频率为 ω 的交变电流驱动下，横向产生出 2ω 的交变霍尔电压 (电流) 信号，如图 1 所示。此乃所谓非线性霍尔效应 (nonlinear Halleffect, NLHE)，并不要求由磁场激发而生，与传统意义上时间反演对称破缺而生的霍尔效应有所不同。从这个意义上，这里的霍尔效应机制，与传统经典物理的载流子驱动过程可能也不完全相同，唯象上更多地类似于非线性光学中的倍频效应。

图 1. 霍尔效应的两种模式：经典熟知的“反常霍尔效应 anomalous Hall effect”和新成员“倍频非线性霍尔效应 nonlinear Hall effect”。图中展示了两种效应背后的动量空间中贝里曲率大小，显示后者贝里曲率偶极 Λ 的巨大变化。

Q. Ma et al, Nature 565, 337 (2019), https://www.nature.com/articles/s41586-018-0807-6

这里，姑且再讨论几句非线性倍频效应：

首先，在非线性光学中，倍频源于空间反演对称破缺的电介质中，偶极子对电磁波中电场分量的非线性响应：因为空间对称性破缺要求，最低非线性响应项就是平方项，因此我们得以在极性光学材料中观测到强倍频效应。这里，电场是极性矢量场，因此倍频效应发生于激发电场相同方向。

其次，对非线性霍尔效应，其严格处理、甚至是半量子半经典的处理，当然都需要求助于量子力学对动量空间能带和载流子输运的深刻讨论。小编不善此道，姑且从唯象理论角度与非线性光倍频效应做粗浅类比，自然有生搬硬套的痕迹，行家里手不必在意这种牵强附会。由此，可以做不严谨的畅想：

(a) 与电场不同，交变电流激发的磁场是轴矢量场，是横向场，因此对激发场的响应必然是在横向上。故而这里的非线性效应根植于横向多项展开，包括线性和二阶非线性的横向霍尔场。

(b) 众所周知，线性霍尔和反常霍尔效应都属于一阶响应，都与磁性相关，打破了时间反演对称。要展示纯粹的二阶非线性霍尔效应，抑制一阶效应就成为必要条件。也就是说，体系需要满足时间反演对称性。满足之，最直接的取舍就是选择非磁性体系。

(c) 既然是二阶及高阶激励，一般意义上电磁激励越强越好。为了避免低阶线性响应而不得不选择非磁性体系，则强化电场非线性响应可能是一个不错的选择，以便提升感应而生的磁场非线性响应。在这方面，非线性光学响应是有意义的参照：选择极性体系，或者至少是非中心对称的体系 (non-centrosymmetry)，有利于非线性响应。

如上唯象意义上的类比讨论，不能作数。用量子力学语言描述才能更为严谨科学。自 MIT 的傅亮老师他们 (2015 年) 提出非线性霍尔效应以来，一批拓扑量子材料人在此耕耘、成就显著。包括我国学者卢海舟团队在内的突出工作，在同行间有重要影响。严格的量子理论，可见诸如卢海舟和杜宗正他们最近的工作(Du et al, Quantum theory of the nonlinear Hall effect, NC 12, 5038(2021), https://www.nature.com/articles/s41467-021-25273-4)。

图 2. 对拓扑量子材料中非线性霍尔效应的量子解释。

(A) 众所周知，无质量的狄拉克费米子，如 (a)所示，具有线性色散和狄拉克锥 (交叉点)，不具有贝里曲率 (no Berry curvature)。如果引入空间反演对称破缺，打开能隙，则在能隙边缘处就会形成较大的贝里曲率，其强弱和正负由图中贝里曲率颜色标度，如 (b) 所示。(B) 如果狄拉克锥发生倾斜或畸变 (tilting)，则费米面附近不同波矢处就有不同的贝里曲率和动量色散，导致巨大的贝里曲率偶极 Λ。取自 Q. Ma et al, Nature 565, 337 (2019),https://www.nature.com/articles/s41586-018-0807-6。(C) 针对外尔半金属，类似的物理展现得更为显著。Type-I 型外尔点附近贝里曲率可能相近。但是，type-II 型外尔半金属中，因为 tilting 导致两个外尔点能量差别，靠近费米面处的外尔点贡献很大的贝里曲率偶极 Λ，与图 (B) 所示物理相似。取自 H. Zheng et al, Adv. Phys X 3, 1466661 (2018),https://www.tandfonline.com/doi/full/10.1080/23746149.2018.1466661。

现在的一些认知是这样的：在非中心对称的非磁性体系 (non-centrosymmetric but time-reversal-symmetricmaterials)，纵向交变电流激发的载流子响应也是非线性的，包含对纵向电场的非线性响应，由此产生了类似的倍频信号。此时，如果将二阶非线性电流分解成半经典项 (时间反演对称) 和与动量空间的贝里偶极矩 (Berry curvaturedipole) 成正比的电流项，则在时间反演对称 (非磁性) 的体系中，二阶非线性霍尔效应，就与贝里偶极矩成正比。由于贝里偶极矩与贝里曲率关于动量的一阶导数成比例，所谓的非线性霍尔效应强弱，就成为动量空间费米面附近、载流子运动时受贝里曲率约束的一个物理考量。简而言之，非线性霍尔效应，就成为动量空间贝里曲率的量度或者结果。图 2 所示乃拓扑量子材料中贝里曲率物理的一些简略示意。

这是拓扑量子材料令人着迷的物理结果：现在不但有了一个新的物理量，来衡量拓扑量子材料中费米面附近贝里曲率大小，而且这一非线性霍尔信号有可能成为某些交变电信号频率转换的潜在应用之源 (这样的应用以前很少让人奢望)。此时，讨论这一信号的大小和强弱，就变得很有意义了，虽然 Ising 尚不敢染指这一话题。

那么，什么体系的贝里曲率(Λ) 会很大？熟悉拓扑量子材料的物理人马上就能回答：外尔半金属体系！动量空间中的外尔点，就如“磁单极”一般，其周围的贝里曲率可能是很大的。

来自日本理化研究所(RIKEN) 的量子凝聚态著名学者 Yoshinori Tokura 和 Naoto Nagaosa 教授领导的团队 (主要作者 Chenglong Zhang 博士已回到中科院物理所任职，主要作者 Tian Liang 博士已回到清华大学物理系任职)，似乎对此颇有心得，最近取得了良好进展。他们将一些最新的结果整理成文，刊登在《npj QM》上，引起同行关注。Ising 后知后觉，对他们的结果学习一二后，罗列如下，部分数据组合在图 3 中：

图 3. 不同成分样品 (Pb_1−xSn_x)_1-yIn_yTe中非线性霍尔效应的测量结果：(A) (B) S36 号样品非线性霍尔电压 V_zx^2ω、纵向倍频电压 V_xx^2ω 与纵向电流 I(ω) 的以来关系。样品测量几何作为插图显示。(C) 不同编号样品的成分 (x~ Sn 含量，y ~ In 含量)。(D) 动量空间的外尔点构型。(E) S33 号样品和 S36 号样品的非线性效应结果，其中 S36 是铁电外尔半金属，而 S33 则不是。

(1) 按照当前的理解，既要非磁性，又要有外尔点，那就最好是非中心对称的非磁性体系才满足要求。好在从 TaAs 开始，一大批非磁性的外尔半金属新材料诞生。这一要求刚好切合 Ising 对极性体系强非线性极化响应的议论。

(2) 非中心对称的外尔半金属，因为空间反演对称破缺，布里渊空间拥有似乎比磁性外尔半金属多很多的外尔点 (pairs)。从能量简并看，太多的外尔点共存，对厘清外尔半金属物理并不方便，也给研究单个外尔态的物理带来复杂性 (例如，体系态密度太高，导致载流子浓度过高，会抑制霍尔效应)，更对利用单个外尔点周围的高贝里曲率引发的非线性霍尔效应不利。看起来，似乎需要关注这一问题，以获得大的贝里曲率和大的非线性霍尔效应。

(3) 前人已经深刻证明，非中心对称的极性外尔半金属，其低阶和高阶偶极作用容易打破外尔点的能量简并 (distorting or tilting)，使得主要是费米面附近的那个外尔点对输运有显著贡献，并使其局域的贝里曲率效应充分发挥出来。小编瞎猜，以为具有强电极性的、空间反演对称破缺的体系，例如铁电外尔半金属体系，应该具备所有这些优点：外尔点倾斜，有利于降低态密度、增强霍尔效应；外尔点倾斜，有利于凸显费米面附近的贝里曲率、增强二阶非线性霍尔效应，如此等等。

Tokura 教授他们成功地找到了 Pb_1−xSn_xTe这一化合物，并在获取巨大贝里曲率和二阶非线性霍尔效应上取得了显著进展。首先，这是一个铁电外尔半金属体系。其次，他们通过 In 掺杂 ((Pb_1−xSn_x)_1-yIn_yTe)，将载流子浓度显著压制到 10^-16 cm^-3的水平，为霍尔效应增强打下了基础。再次，他们实现了高达 10^-21 m³的贝里曲率偶极密度(Berry curvature dipole density)，令人印象深刻，比前人的结果高数百到数百万倍 (10² ~ 10⁷)。最后，他们还提炼出“磁单极”附近贝里曲率与波矢 k 成平方反比 (k^-2) 关系的规律，揭示出铁电外尔半金属具有实现巨大贝里曲率偶极密度和非线性霍尔效应的潜力。

行文至此，可以看到这是一项富有成效的工作。作者成功地找到了一种取多方宠爱于一身的铁电外尔半金属体系。在此基础上，这一工作既深化了非线性霍尔效应作为贝里曲率量度的物理内涵，更展示了未来利用这一物理效应的应用潜力。当然，这里显示的，依然是较低温度下的结果，铁电极化对贝里曲率的调控效果显示得也不那么清晰。而提升温度、提升效应、进而展示一个给同行希望的器件原型，应该是作者和读者的期待和目标。

雷打不动的结尾：小编是外行，如若理解错了，敬请谅解。各位有兴趣，还是请前往御览原文。原文链接信息如下：

Giant Berrycurvature dipole density in a ferroelectric Weyl semimetal

Cheng-Long Zhang, Tian Liang, YoshioKaneko, Naoto Nagaosa Yoshinori Tokura

npj Quantum Materials volume 7,Article number: 103 (2022)

https://www.nature.com/articles/s41535-022-00512-z

沁园春·新年

楼外微尘，巷底潺流，日月露眠

瞰水波凝重、枯枝色简，秦淮风凛、文庙凋寒

大道平庸，轩窗落寞，本应繁华南北喧

阴阳事，断无从回首、未允余欢

终归劫过三年

莫忘却、蹉跎家国言