如图所示，有一个水平长度为4、高度为3的两阶楼梯，它的阶梯总长为3+4。如果使阶梯变小，但增加阶梯的数量，它的总长仍然是3+4。然而，如果阶梯的数量是无穷的，最后它就变成了一条线，它的总长仍然是3+4。但是，根据勾股定理，我们可以算出这条线的长度为5，所以我们就得出3+4=5的错误结论，这个问题被称为楼梯悖论。

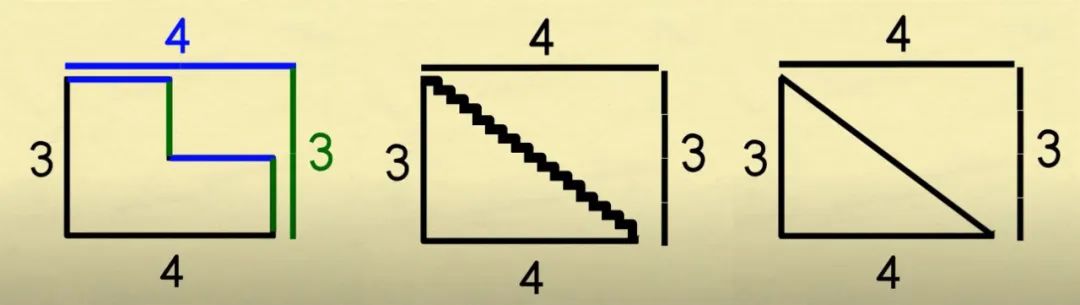
很多人都知道，这是因为折线和直线之间存在误差。但如果仅仅认识到这一步，总感觉这个问题不能得到很好的解释。例如，我们在用任意曲线积分求面积时，老师就教我们用无穷多的细矩形进行代替，但二者之间也是存在误差的。那为什么积分求面积就成立，而楼梯悖论就不对呢？

事实上，问题就在于，无限多个小误差累积起来会不会变成一个大误差。简单来说，积分求面积时的误差是两个无穷小长度的平方，即二阶无穷小。对它进行一阶无穷多次累加之后，我们得到的仍然是一阶无穷小。而对于所谓的楼梯悖论来说，它的误差是无穷小长度，即一阶无穷小，经过无穷多次累积后就可能变成一个可观的误差，所以折线不能用斜线代替。

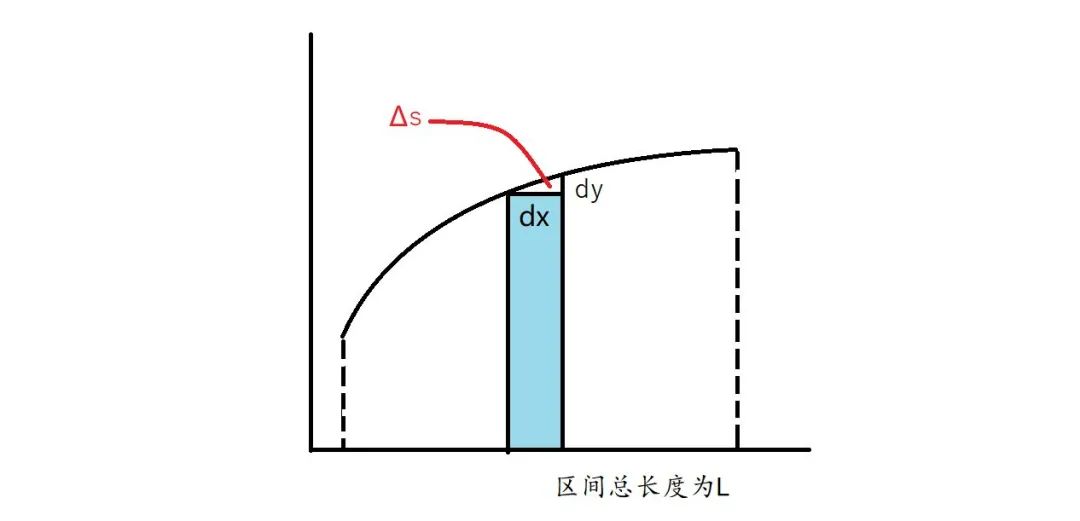
如果只是用上述的语言进行描述，那么有些人可能还有点怀疑，那么下面我们就用一个例子来给大家一个直观的感受。如上图所示，误差面积为三角形Δs=dx·dy。我们令dy=k·dx，其中k为斜率，那么Δs=k·dx²。因为dx=L/n，所以Δs=k·(L/n)²。那么，把n个小误差累加起来，我们就得到：

所以，当n趋近于无穷时，总的误差S就趋近于零。

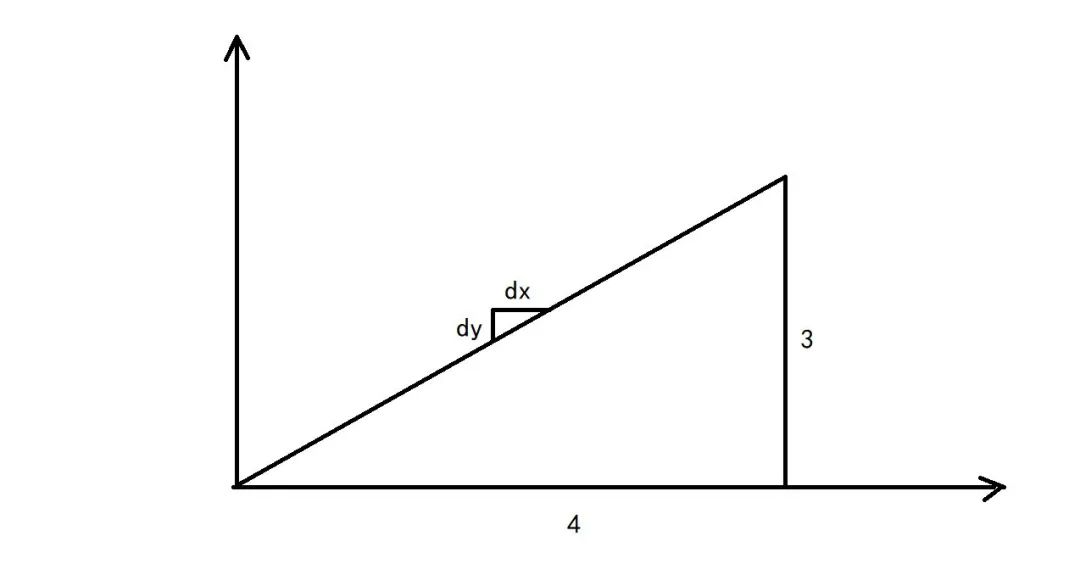
接下来，我们来看看所谓楼梯悖论的误差。如上图所示，小直角三角形处的长度误差ΔL=dx+dy-(dx²+dy²)^0.5。因为dy=(3/4)·dx，我们就有ΔL=dx/2。同样，dx=4/n，所以ΔL=2/n。那么，把n个误差累加起来，得到总误差：

所以，当n趋近于无穷时，我们不能把折线看成是斜线处理，并且它们之间的差总是等于2。

转载内容仅代表作者观点

不代表中科院半导体所立场

编辑：六块钱的鱼