0 引言
随着我国工业化水平不断地提高,地铁车辆已经成为代步的主要交通工具,应用到各个城市中。电机作为地铁车辆驱动系统的重要部分,其控制技术决定了地铁运行性能的重要指标,该技术也成为研究的热点
PSO 优化算法编程简单、收敛快等优点,采用该控制技术对PMSM 进行动态控制可以弥补传统PI 控制的缺陷。
本文在电机PI 控制的基础上将粒子群算法应用到“转速- 电流”双闭环PI 参数优化中,能快速逼近最优参数,实现地铁车辆永磁同步电机运行跟平稳,系统精确性跟好。
*基金项目:湖南工业大学研究生创新基金项目“级联STATCOM 控制策略及应用研究”(课题编号:CX1811)
作者简介:刘安海(1994—),硕士研究生,主要研究方向为车载电子与电器。
黄星(1995—),主要研究方向为电网节能和降耗。
龚星宇(1996—),主要研究方向为电力网络优化与控制。
通信作者:于惠钧(1975—),男,教授,硕士生导师,研究发现为系统保护与自动化技术。
1 PWSM在d-q坐标系下的数学模型
1.1 坐标变换
为了使PMSM 拥有直流电机的性能,利用坐标变换简化数学模型

式中:θ 是转子位置角。
1.2 永磁同步电机的数学模型
对PMSM 的数学模型进行推导过程中,其数学模型建立假设前提有[15]:
1) 永磁体材料的电导率为0;
2) 忽略齿槽和电枢反应影响;
3) 转子上没有阻尼绕组;
4) 定子各绕组互差120° ;
5) 各相绕组是正弦波形;
6) 各绕组的电感和电阻为定值。
上述前提推导下,数学模型电压、磁链和转矩方程为

式中: u
其机械运动方程为

式中: TL 是负载转矩, B 是阻尼系数, J 是转动惯量,ω 是电角速度。
2 永磁同步电机矢量控制系统
在dq 坐标系下,永磁同步电机的转速和转矩控制变为对电流分量isd 、isq 直接控制,采用isd = 0 ,使转矩波动很小
当定子电流在d 轴上的分量为0 时,电机电压、磁链和转矩方程为

根据式(13) 可知电机的电磁转矩Te 只与电流分量i
图1 是面装式PMSM矢量控制系统图,也是“电流-速度”双闭环调速控制图,提高了控制精度,减小误差干扰。通过检测转子位置,来控制IGBT 开关管的开关状态,使is 在d 轴上的分量为0,则输出转矩平稳

图1 永磁同步电机矢量控制系统
转速环将参考转速1 500 r/min 和电机实际转速比较,其转速误差经过速度PI 控制器,得到电流分量isq与实际电流比较,令isd=0。比例积分传递函数G(s) 为

式中:Kp、Ki 为比例和积分系数。
3 粒子群算法的控制器
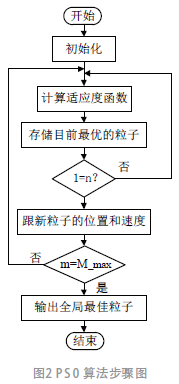
在仿真过程中,模型和参数会有所不同, 电机性能也会有所降低。在系统初始阶段一般根据经验微调PI参数,然后在PID 控制的基础上引入PSO 控制器来调整PI 参数。粒子群算法在解空间中找到最优的粒子来实现PI 参数整定,具有较好的收敛速度和寻优精度,如图2 是它的步骤图。我们假设在K 维目标搜索空间中每n 个粒子构成一个种群,每个粒子以给定的速度寻找最佳位置,它会根据自己现在的位置和历史上的最佳记录位置来更新自己的位置,粒子群优化需要不断更新粒子的速度和位置
采用PSO 算法对PI 控制参数的优化,其中粒子L的当前/ 电流位置表示为:

粒子L 的当前速度表示为:

在其搜索历史中粒子L 最佳位置为:

粒子在其搜索历史中的最佳位置为:

通过以下公式更新速度和位置:
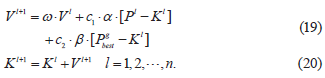
式中,α,β 是(0,1)的随机数,ω 是恒定惯性权重,c
4 仿真结果与分析
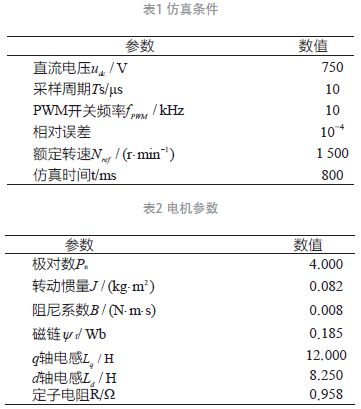
为了验证粒子群算法比传统PI 控制器优化效果跟好,搭建仿真模型,给出的仿真条件和电机参数如表1、2 所示。
4.1 PMSM转速仿真
转速环PI 参数K
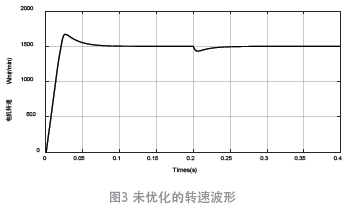
电机启动0.06 s 后稳定到参考转速1 500 r/min,且转速超调量较高会缩短电机寿命。为了提高控制性能,通过粒子群算法得到更优PI 参数值是必需的。图4 是粒子群算法控制器与传统PIK 控制器仿真对比图,从图中可知,转速稳定跟快,超调量几乎为0。

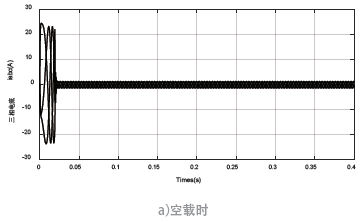
仿真模型空载和负载下仿真,图5 是三相定子电流波形,由图5a) 可知,空载启动时电流脉动很快就稳定下来了。由图5b) 可知,在0.2 s 时加入负载后,定子电流在0.03 s 才稳定下来,比空载时达到稳定用时更长。

仿真模型空载和负载下仿真,图6 是电磁转矩曲线。

从图6 可以看出,电机刚启动时电磁转矩有较小波动,空载条件下约0.03 s 时,电磁转矩达到相对稳定,负载条件下约0.035 s 时,电磁转矩与负载转矩达到平衡,转矩良好,说明抗干扰的能力较强。
综合上述分析,当永磁同步电机参考转速为额定转速的情况下,无论是在空载条件下还是负载条件下运行,使用粒子群优化算法的控制效果明显较好。
5 PMSM基本工况仿真
5.1 启动特性仿真
首先,设置启动转速为1 500 r/min, 在0.2 s 加速到3 000 r/min,0.32 s 达到额定转速。图7 是电机转速、三相定子电流和电磁转矩仿波形。其中图7a) 是从静止启动,0.07 s 时转速稳定到了1 500 r/min,然后进行匀速运行。在0.2 s 时开始加速运行,大约0.32 s 时转速稳定到3 000 r/min。

根据图7c) 可知,在0.07 s 时三相定子电流幅值稳定到一固定值,在加速过程中也一样,同时电磁转矩曲线随着转速的稳定迅速稳定到0,从图7b) 电磁转矩仿真波形可知,电磁转矩对负载转矩响应良好,图7 也能看出采用粒子群算法优化后波形要比传统经验获得的PI参数得到的波形平稳很多。
6 制动特性仿真
由于地铁车辆经常会启动加速和制动减速频繁等特点,良好的制动性能是地铁车辆的一个重要标志。因此,制动性能的好坏体现了永磁同步电机稳定情况,采用调速方法的好坏,所以系统更需要良好的制动性能。地铁启动的参考转速为1 500 r/min,负载转矩15 N.m。在0.2 s时,设置负载转矩突变为20 N.m;在0.3 s 时,设置参考转速突变为0 进行制动。从图8 可看出电机转速没有超调量,电磁转矩和三相定子电流也跟随转速变化有良好的响应。

7 结论
本文研究了在地铁车辆运行中,为了永磁同步电机转速更好控制,采用“转速- 电流”双闭环、isd = 0 的矢量控制策略,在构建了矢量控制系统的基础上增加了粒子群算话(PSO) 优化控制器参数的控制思想,并对地铁车辆在不同工况下的启动、制动性能,调速性能进行分析。根据仿真结果可知,通过采用粒子群算法优化控制系统PI 参数后,电机转速的超调量几乎为0 并快速稳定到参考转速,电机输出振荡小,抗干扰能力强,得到了优化效果。
参考文献:
[1] 朱健,曹君慈,刘瑞芳,等.电动汽车用永磁同步电机铁心采用非晶合金与硅钢的性能比较[J].电工技术学报,2018,33(2):353-354.
[2] 胡小林.永磁同步电机控制器参数自整定技术研究[D].成都:西南交通大学,2018.
[3] 高灵霞,孙凤兰.无刷直流电机的自适应模糊滑模控制策略研究[J].测控技术,2015,34(12):78-82.
[4] MENDOZA-MONDARGON F,HERNANDEZ-GUZMANV M,RODRIGUEZ-RESENDIZ J.Robust speed control of permanent magnet synchronous motors using twodegrees-of-freedom control[J].IEEE Transactions on Industrial Electronics,2018,65(8):6099-6108.
[5] 郑美茹,王圣,王丰,等.基于分数阶次符号函数的永磁同步电机滑模控制技术[J].电工技术学报,2017,32(9):56-62.
[6] 高旭东,许鸣珠,栾东雪.基于DSP的永磁同步电机调速控制研究
[J].控制工程,2017,24(7):1318-1319.
[7] 廖雄志,文定都,湛政,等.基于模糊 PID 的永磁同步电机调速系统[J].湖南工业大学学报,2018,32(2):27-28.
[8] 白天明.基于新型扰动观测器的永磁同步电机滑模控制[J].电机与控制应用,2016,43(9):20-21.
[9] ANTONELLO R,CARRARO M,ZIGLIOTTO M.Maximumtorque-perampere operation of anisotropic synchronous permanent-magnet motors based on extremum seeking control[J].IEEE Trans. Ind. Electron,2014,61(9):5086-5093.
[10] ZHANG Z,ZHOU H,DUAN J A,et al.Research on Permanent Magnet Linear Synchronous Motors With Ring Windings for Electromagnetic Launch System[J]. IEEE Transactions on Plasma Science,2017,45(7):1161-1167.
[11] LI B,ZHAO J, LIU X,et al.Detent Force Reduction of an Arc-Linear Permanent-Magnet Synchronous Motor by Using Compensation Windings[J].IEEE Transactions on Industrial Electronics,2017,64(4):3001-3011.
[12] 邹敏,文定都,何宗卿,等.基于前馈补偿的模糊PI永磁同步电机调速系统[J].湖南工业大学学报,2019,33(03):35-40.
[13] 赵钢,成丁雨.电动汽车永磁同步电机工况仿真分析[J].自动化仪表,2016,37(2):5-6.
[14] 赵辉,胡仁杰.SVPWM的基本原理与应用仿真[J].电工技术学报,2015,30(14):350.
[15] 王明明,刘云浩,孙晓云.地铁车辆用永磁同步电机的转速控制[J].济南大学学报,2019,33(4):326-327.
[16] 艾青,陈功贵.电动汽车用永磁同步电机调速系统研究[J].牡丹江大学学报,2012,21(2):147-149.
[17] 刘彦呈,任俊杰,王宁,等.永磁同步电机旋转坐标系滑模观测器设计研究[J].电机与控制学报,2015,19(7):36-44.
[18] DURSUN M.The analysis of different techniques for speed con-trol of permanent magnet synchronous motor[J].Tehnicki Vjesnik,2015,22(4):947-952.
[19] CAO S,JI T,LIU H.Pso algorithm-based robust design of pid controller for pmsm[C].Sixth International Conference on Natural Computation,2011:3513-3517.
(本文来源于《电子产品世界》杂志2021年3月期)

