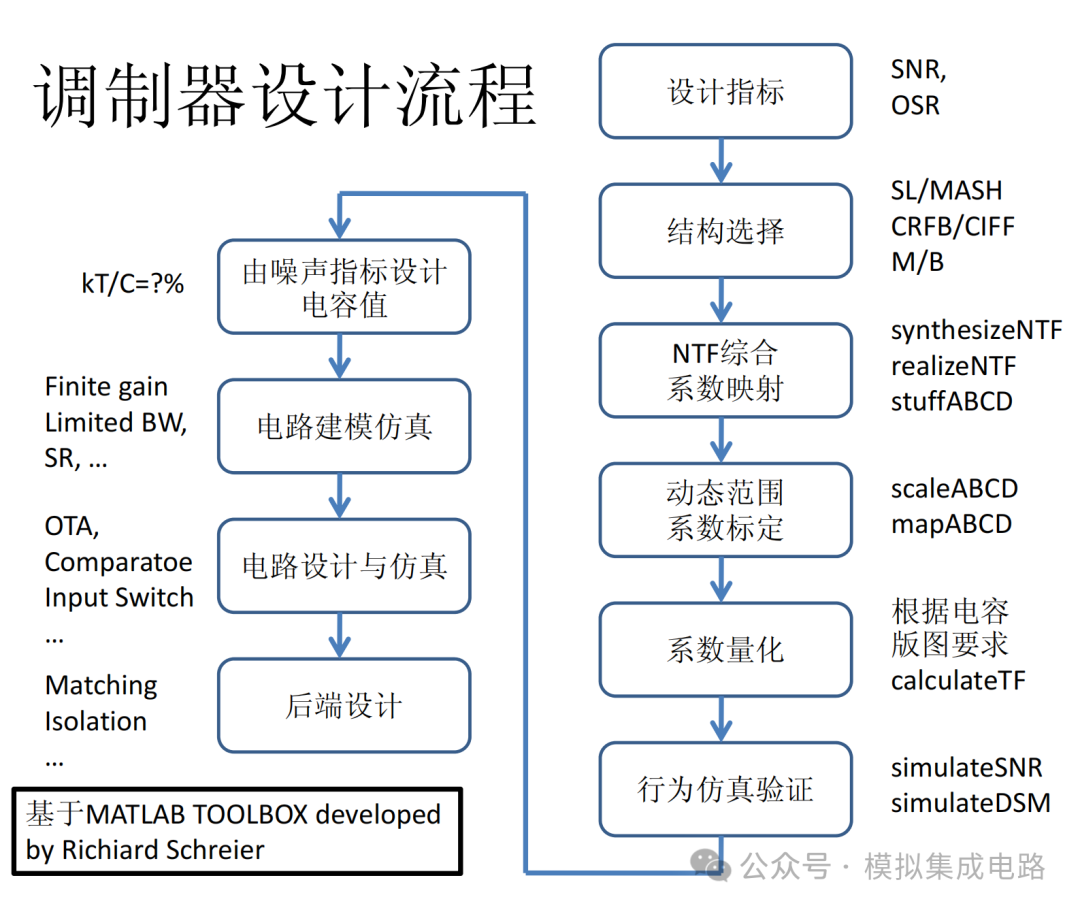
通过matlab工具将delta sigma调制器设计流程化，能够优化设计人员的设计流程，减少工作量。下面介绍一下matlab 工具。

1、下载delsig

转至 http://www.mathworks.com/matlabcentral/fileexchange/ 并搜索 delsig，下载并安装 delsig.zip 文件。将 delsig 目录添加到 MATLAB 路径。要提高仿真速度，请在 MATLAB 提示符下键入 mex SimulateDSM.c 来编译 SimulateDSM.c 文件。对simulateMS.c 执行相同的操作。

在运行函数时，matlab会报warning，如下：

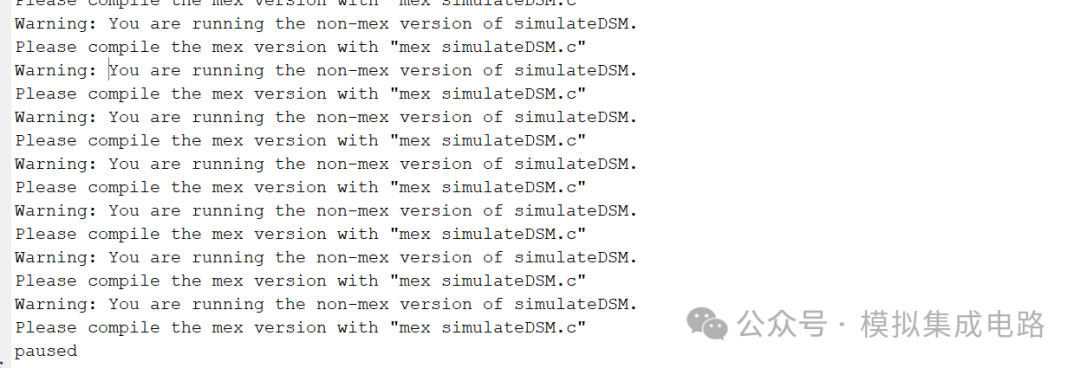
当我们使用“ mex simulateDSM.c”的时候会报没有minGW编译环境的错误。这时我们需要根据matlab提示，在附加功能里面下载安装“mingw.mlpkginstall"，右键以matlab运行这个程序，matlab会自行安装minGW环境。

再切换到delsig目录下，运行编译命令，即可完成编译。

2、介绍delsig

在delsig文件夹下有个DSToolbox.pdf的文档，文档中有详细的英文介绍。本内容简单的截取部分内容。

2.1、dsdemo介绍：

dsdemo1:SynthesizeNTF 函数的演示。具有和不具有优化零点的 5 阶低通调制器以及具有优化零点的 8 阶带通调制器的噪声传递函数合成。

dsdemo2:演示simulateDSM、predictSNR和simulateSNR功能：时域模拟、使用Ardalan和Paulos的描述函数方法预测SNR、频谱分析和信噪比计算。给出了低通、带通、多位低通示例。

dsdemo3:演示NTF、stuffABCD、scaleABCD和mapABCD功能的实现：系数计算和动态范围缩放。

dsdemo4:使用 抽取的 MOD1 和 MOD2 的音频演示。

dsdemo5:SimulateMS 功能演示：失配整形 DAC 的元件选择逻辑的仿真。

dsdemo6:designHBF功能的演示。高效的半带滤波器硬件设计和仿真。

dsdemo7:findPIS 函数的演示：正不变集合计算。

dsexample1:离散时间调制器设计示例。

dsexample2:连续时间低通调制器设计示例。

2.2、函数介绍

综合一个噪声传递函数：

ntf=synthesizenNTF(order,R,OPT,H_inf,f0)
order: NTF的阶数。对于带通调制器，order必须是偶数。
OSR:过采样率。
opt:优化NTF零点的标志。

将噪声传递函数转换为指定的拓扑结构:

[a,g,b,c]=realizeNTF(ntf,form='CRFB',stf=1)
ntf:调制器的NTF，以零极点的方式给出。
form:指定调制器的拓扑结构。
stf:调制器的STF，定义为zpk的对象。
a,g,b,c:输出调制器的参数。

根据指定拓扑的参数计算ABCD矩阵:

ABCD=stuffABCD(a,g,b,c,form='CRFB')

将ABCD矩阵转换为指定拓扑的参数:

[a,g,b,c]=mapABCD(ABCD,form='CRFB')

对由ABCD矩阵描述的 调制器执行动态范围缩放:

[ABCDs,umax]=scaleABCD(ABCD,nlev,f,xlim,ymax)
ABCD:调制器环路滤波器的状态空间描述。
nlev:量化器的电平数。
f:测试正弦信号的归一化率。
xlim:对状态的限制，可能是一个向量。
ymax:判断调制器稳定阈值。如果量化器输入超过ymax,则认为调制器不稳定。

假设量化器增益为k,计算由给定ABCD矩阵描述的调制器的NTF和STF:

[ntf,stf]=caculateTF(ABCD,k=1)

3、使用相关函数

使用上述相关函数完成对CIFB结构调制器参数求解，并进行调制器进行缩放，通过仿真来查看调制器状态变量的范围。代码如下：

echoon
order=3;OSR=64;opt=0;H_inf=1.5;f0=0;nlev=17;%定义参数。
echooff
H=synthesizeNTF(order,OSR,opt,H_inf,f0);
[a,g,b,c]=realizeNTF(H,'CIFB');%将NTF转换成为特定调制器拓扑的一组系数。
b=[b(1),zeros(1,length(b)-1)];%Useasinglefeed-infortheinput
ABCD=stuffABCD(a,g,b,c,'CIFB');%转成空间矩阵
[ABCDs,umax]=scaleABCD(ABCD,nlev,f0,[8],[10]);%缩放空间矩阵
ABCDs
[as,gs,bs,cs]=mapABCD(ABCDs,'CIFB');%将缩放后的空间矩阵映射成调制器的系数

x=linspace(0,umax,20);
N=4096;%仿真点数
t=ones(1,N);%一行n阶矩阵
maxstate=zeros(order,length(x));
fori=1:length(x)
xi=x(i);
[v,xn,xmax]=simulateDSM(xi(t),ABCD,nlev)%仿真调制器
maxstate(:,i)=xmax(:);
end

figure(1);clf
fori=1:order
plot(x,maxstate(i,:),'o');
holdon
plot(x,maxstate(i,:),'-');
end

x=linspace(0,umax,20);
N=4096;
t=ones(1,N);
maxstate=zeros(order,length(x));
fori=1:length(x)
xi=x(i);
[v,xn,xmax]=simulateDSM(xi(t),ABCDs,nlev)
maxstate(:,i)=xmax(:);
end

figure(1);
fori=1:order
plot(x,maxstate(i,:),'x');
holdon
plot(x,maxstate(i,:),'--');
end
a
g
b
c
as
gs
bs
cs

计算出来的缩放后的系数：

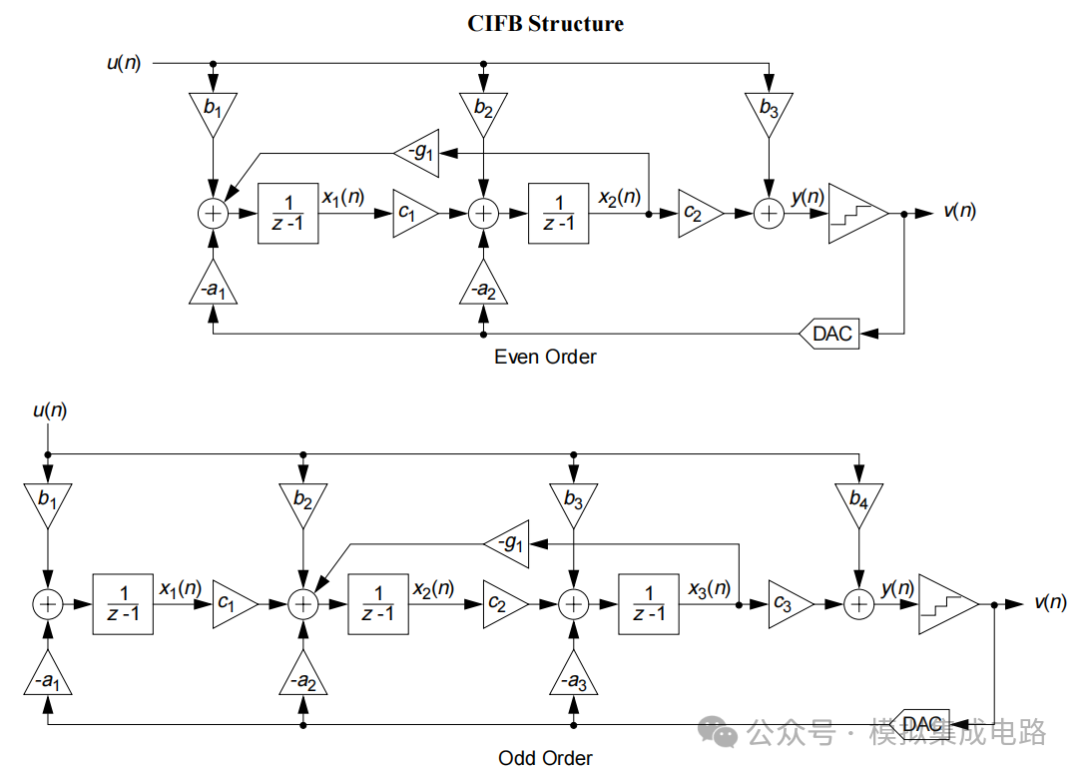
我们求解出缩放后的参数就可以对应相应的结构中：

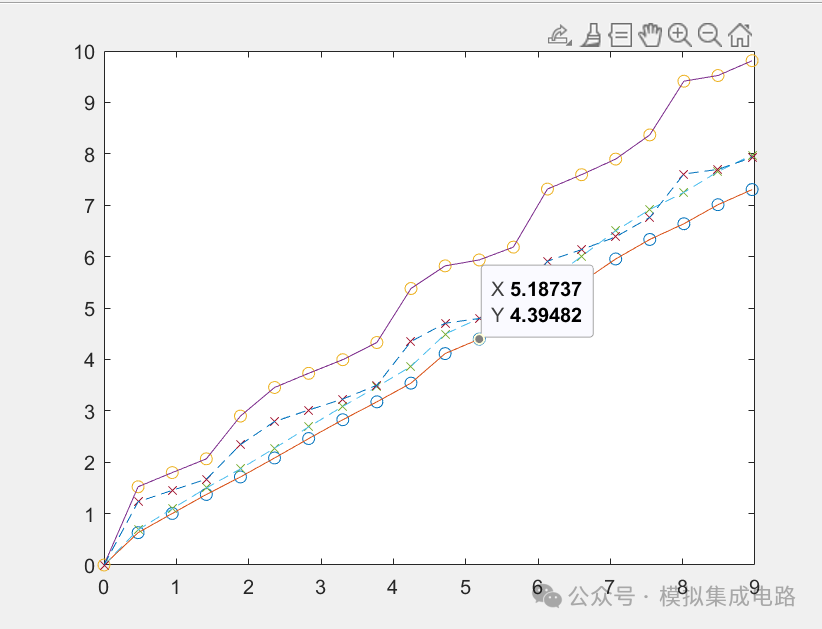
调制器状态变量范围仿真图：