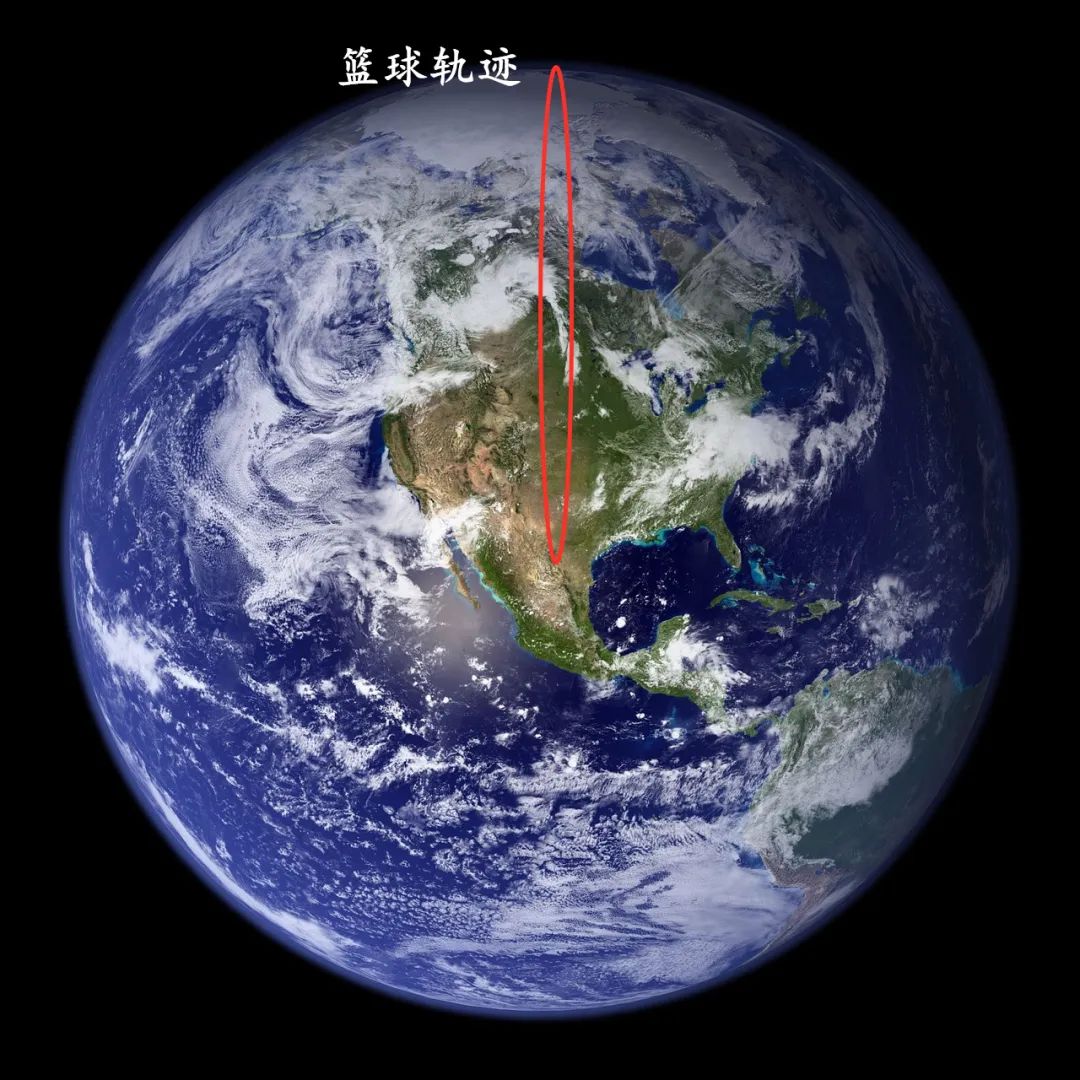
如果我问你，在忽略空气阻力而只考虑地球引力的情况下，投出去的篮球在空中的轨迹是什么？相信很多人都会说是抛物线。我们之所以会这样认为，是因为这种抛体运动有一个重要的近似，就是地球是一个无限大的平面，而且重力在任何地方都是恒定且垂直向下的。

但事实上，如果没有地面的阻挡，篮球会一直向地心奔去，在绕过地心后又会返回原来的位置。篮球飞行的轨迹是偏心率比较大的椭圆，而我们看到的地面上的轨迹只是椭圆的一小部分。

那么，为什么我们能把椭圆当成抛物线来处理呢？在高中时，我们就已经能在物理上找到这种近似处理的合法性。但是，在数学上这种近似为什么是可接受的？这困扰了我整个高中时期，毕竟当时我们所熟悉的抛物线方程和椭圆方程相差太大。

要解决这个问题，我们不能使用直角坐标，取而代之的是使用极坐标。为此，我们要先来推导极坐标系下的圆锥曲线方程。圆锥曲线的定义是，动点P到一定点F的距离r，动点P到一准线的距离为d，两个距离之比为一常数 e(偏心率)，即r/d=e。那么，该动点P的轨迹就是圆锥曲线。根据这一定义，我们以定点F为极心，可以画出如下图形。

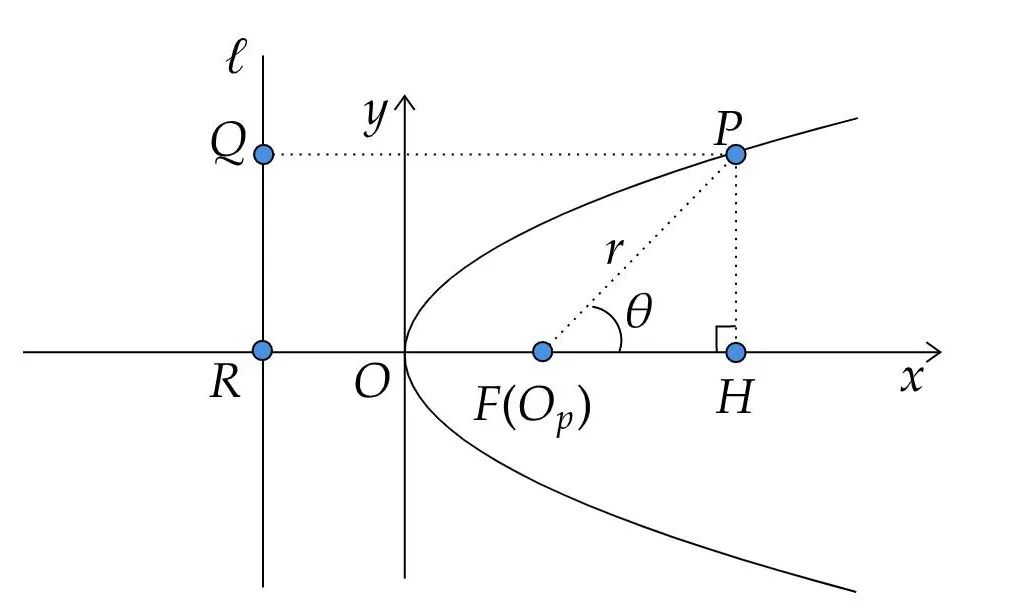
从图中我们可以得到，通常我们将准线到焦点的距离称为准焦距p，即。这样一来，我们就可以根据圆锥曲线的定义写出如下等式：。于是，我们就能得到极坐标系下圆锥曲线的方程。

接下来，我们谈论不同的偏心率e所对应的圆锥曲线。当e=0时，此时曲线为圆（它的准线在无穷远处）；当0<e<1时，曲线为椭圆；当e=1时，曲线为抛物线；当e>1时，曲线为双曲线。

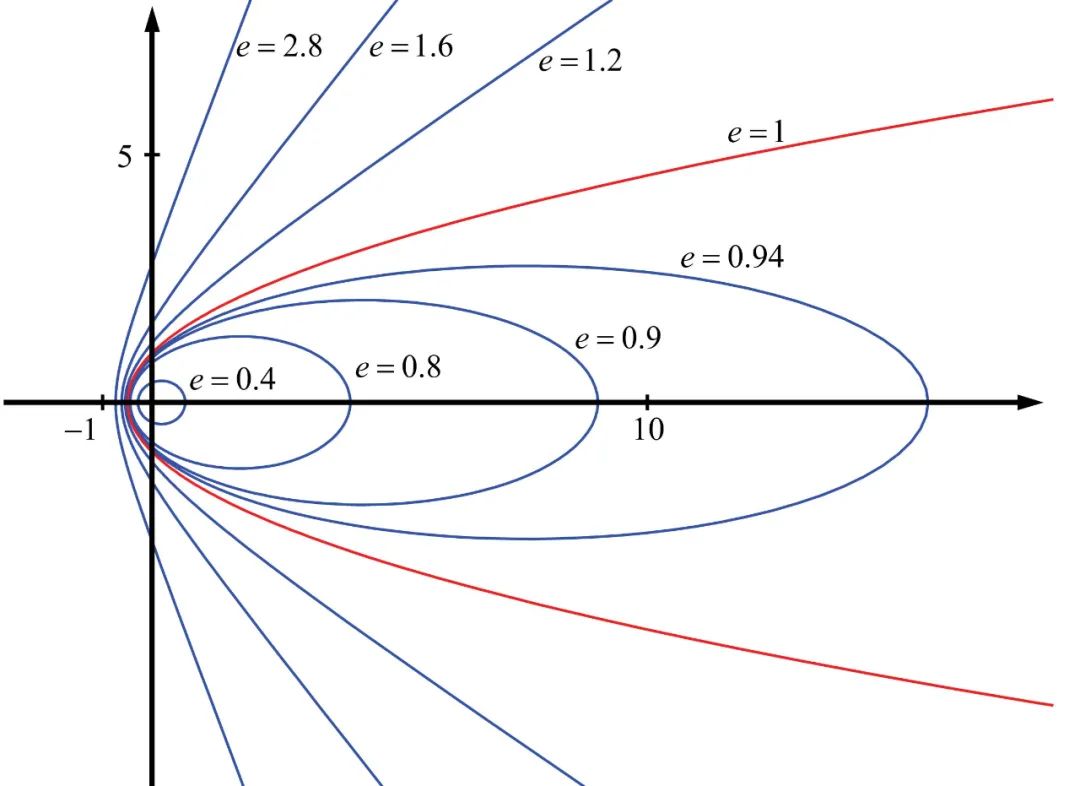
回到我们开头所谈的篮球轨迹，其真实轨迹为椭圆，且篮球的折返点基本与地心重合。根据椭圆偏心率的定义，我们可以知道在这种情况下，此时篮球轨迹所形成的椭圆偏心率e与1相差无几，极限情况下我们可以取e=1。而e=1所对应的圆锥曲线就是抛物线，所以我们可以用抛物线来近似椭圆。

文章内容仅代表作者观点
不代表中科院半导体所立场

编辑:静玲子