反常霍尔招摇处，半源外尔半源磁-icspec

反常霍尔招摇处，半源外尔半源磁

来源:中科院半导体所发布时间:2023-02-24

分享至微信

来源：Ising

作者：量子材料QuantumMaterials

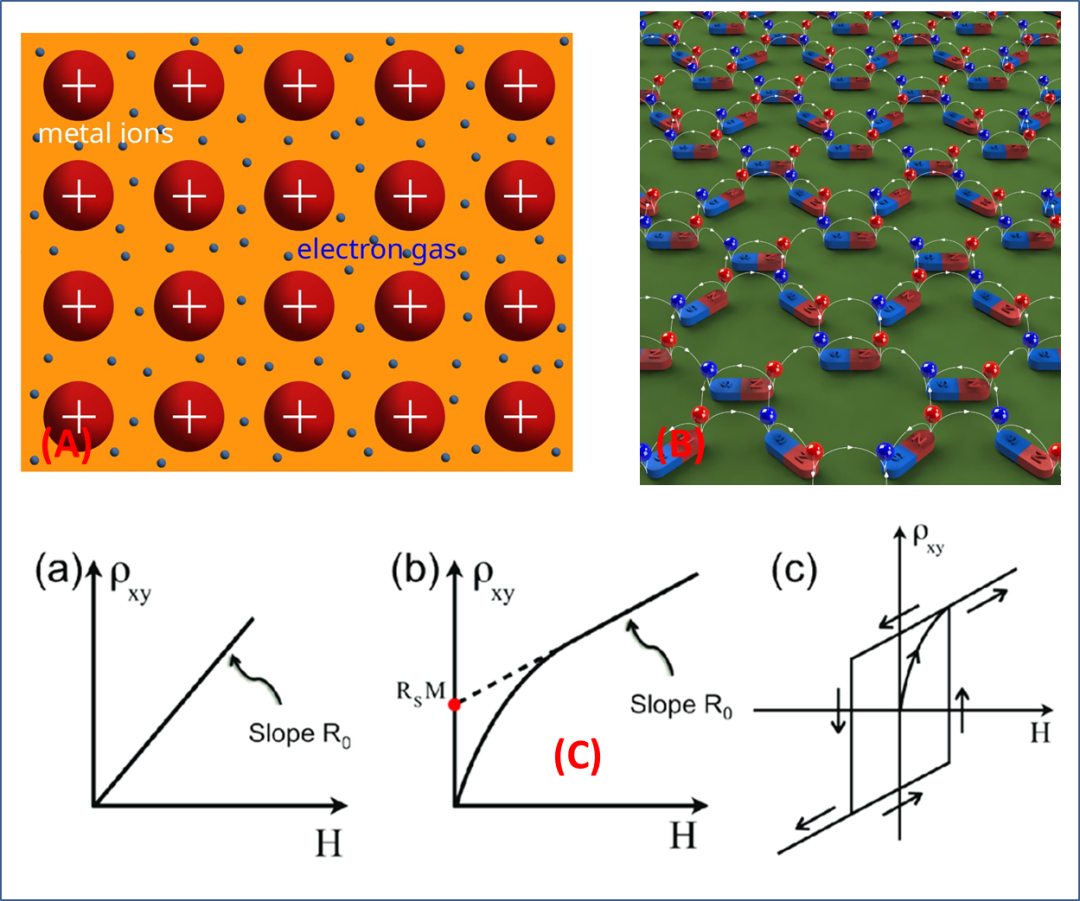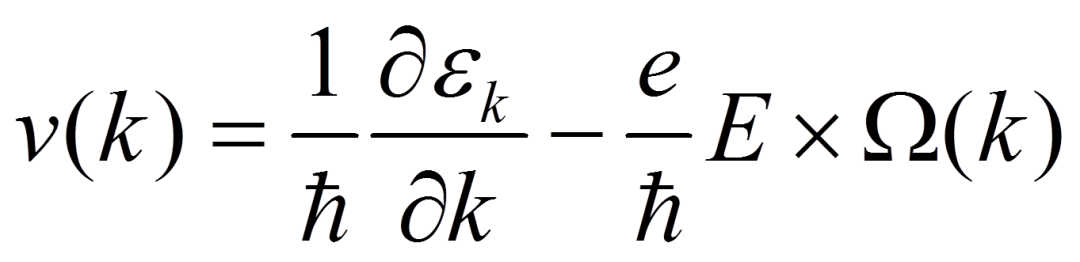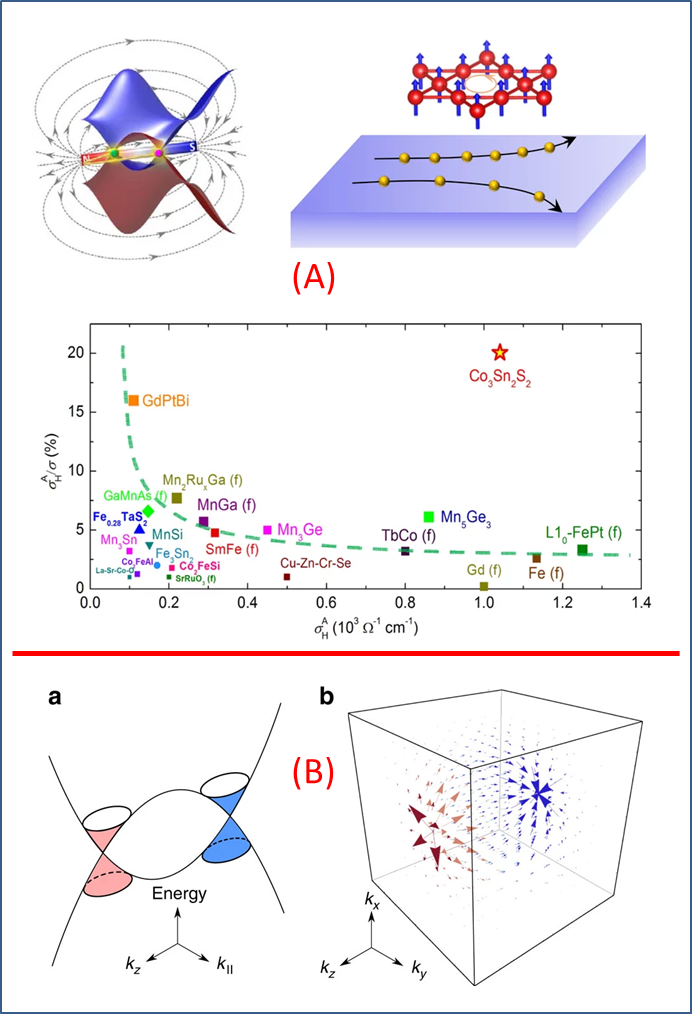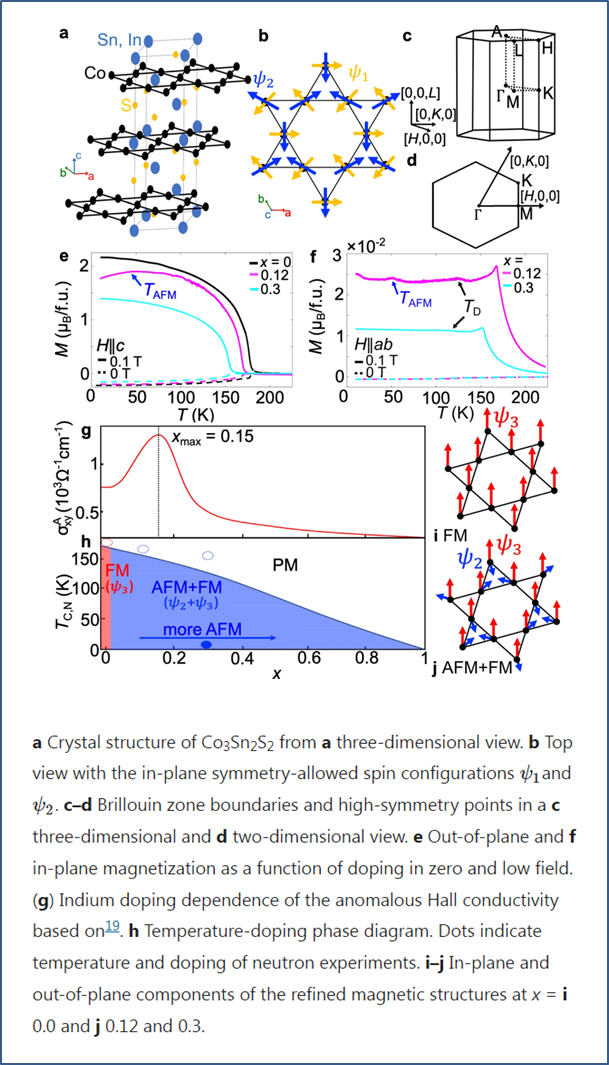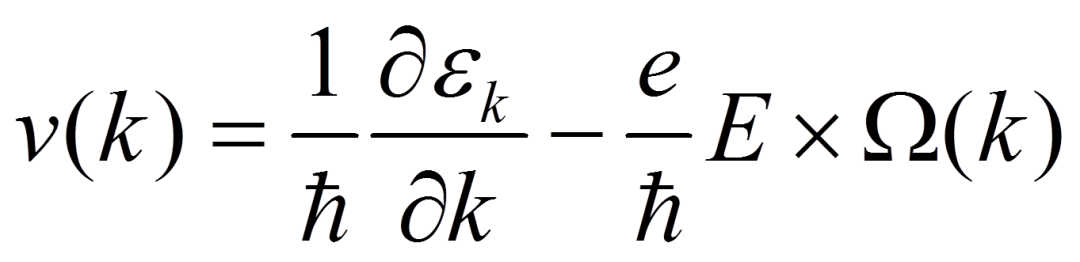
Ising 讲授物理系的《电磁学》课程多年。期中、期末考试命题时，总会开动脑筋与那些聪明的同学们“斗智斗勇”。除此之外，也偶尔会开动脑筋想一想的就是心目中的电磁物理了。想一想还有哪些在前辈同道的教材中呈现得不多、或至少没有被作为主要内涵呈现的现象？想一想为什么电磁之间那么多“细枝末节”？微不足道中的细微之一，便是电子携带的电荷能量比其携带的自旋或者磁能量要大很多。这一结论众所周知，通过比较一个电子电荷的电能和比较一个基本磁矩的磁能，即可确认。也因此，人类对电的运用，比对磁的运用，要广泛和精深得多。当然，因为地球壳层中存在大量铁的氧化物、硫化物甚至单质等 (比例可能达 30 % 以上)，我们的祖先接触磁比接触电要早很多。这种早接触的原因，不过是磁性物质在地球上到处都是、随手可取而已；但电的取用，却得之不易。

即便如此，对磁性的运用，却远没有对电的运用发展得快。磁性因为弱，也因为磁场的轴矢量特征，近现代自然科学对相关效应的认识显示，磁场呈现横向 (叉乘) 作用特征。叉乘物理 (磁)，比点乘物理 (电)，理解和掌握起来要困难得多，也导致磁学应用落在电学应用之后。这些差别，在很多物理人看来，亦或是小事或谬论，但也可能被拿来为科普一些新物理效应提供铺垫。图1 (A) 和 (B) 显示了固体中的一些和电荷和人工磁荷的图像。

最能体现磁和电相对强弱对比的物理效应，当然是霍尔效应，特别是反常霍尔效应(anomalous Hall effect, AHE)。注意，一般情况下，AHE 比正常线性霍尔效应要强大很多，如图 1 (C) 所示。霍尔效应，最典型的特点，便是将电场作用下的纵向电荷输运，通过外加磁场或内禀磁场作用，转换为横向电荷输运 (叉乘)。比较纵向电功率和横向电功率，就能直接衡量出电性和磁性在能量上的相对强弱。事实上，对金属或窄带半导体稍有了解的物理人，即可得出印象：电性比磁性的确强大得太多！一般情况下，霍尔信号多在微伏或毫伏。对应的洛伦兹力驱动电荷运动的动能，比电荷本身携带的静电能小太多了。

图1. (A) 晶体中电荷及其运动，其中电子携带的电能比电荷运动形成的磁能要大得多。(B) 人工自旋冰阵列中每一个软磁棒两端是正负磁荷或“磁单极”(红点和蓝点)。(C) 正常线性霍尔效应 (a) 和反常霍尔效应 (b)，其中的霍尔回线显示于 (c) 中。

(A) https://www.tec-science.com/material-science/structure-of-metals/lattice-structure-of-metals/

(B) https://newsroom.niu.edu/scientists-create-rewritable-magnetic-charge-ice/

既然如此，那好吧，就开始有物理人不信邪，非要在如何产生出很强的磁效应中做文章不可。这算是 Ising 强行扯在一起的、物理人追求拓扑量子体系中巨大反常霍尔效应 (giant anomalousHall effect, giant AHE) 的理由。

读者可能觉得这一步跨度太大，难以衔接它们：为何从 giant AHE 一步就跨到了拓扑体系？这里的内在物理联系，大概有如下几点：

(1) 电性能很强大，在一定程度上与电荷的极矢量特性和球对称电场有关。而且，这种满足库仑定律的极矢量场，可能是付诸实际应用最合理和可控性最成熟的模式。果若磁性也能形成某种“极矢量”场，实现巨大磁效应可能就有机会，例如巨反常霍尔效应。注意，这里只提反常霍尔效应而不理正常霍尔效应，乃是因为通过产生巨大外磁场去实现大的霍尔效应没有在这里讨论的意义。

(2) 既然如此，那就见样学样，去寻找磁单极物理。当然，近现代磁学早就判定，磁性的起源只是电性的电动力学后果而已，磁单极不大可能存在。然而，总是有些物理人不甘放弃，前赴后继，继续寻找“不可能”的磁单极或者“赝磁单极”。这其实是后来诞生的实空间烧绿石氧化物自旋冰物理的一个出发点，如图 1 (B) 所示：两进两出的自旋冰，存在“三出一进 (正磁荷)”和“三进一出 (负磁荷)”的低能激发态。这一对激发态就等效为一对正负磁单极，被类似于电场线的狄拉克弦 (Diracstring) 联系着。毫无疑问，围绕着这一个磁单极的周围，就是等效磁场最大的空间区域。

(3) 不过，这样的实空间自旋冰，只是一个类比而以，目前来看还缺乏明确的学科意义和应用目标。量子材料人自然不会放弃，努力的结果，就是另外一种出自于波矢空间的“磁单极”。熟悉拓扑物理的人早就知晓，波矢空间中的外尔半金属就有一对一对的外尔点：在布里渊空间的每一个外尔点位置周围，充满了贝里曲率 (Berry phasecurvature) 的径向散度分布。而贝里曲率就类似于一个梯度场，就像电荷周围的电场分布一般，或许也可以用散度高斯定律描述^_^。

(4) 好吧，这看起来很漂亮，只是毕竟不是电场分布，而是贝里曲率分布而已，因此跟磁单极之间的联系不那么物理。不过，载流子输运的半经典运动方程很早就揭示给我们：所谓贝里曲率，就是动量空间的磁场，正如下面的方程所示。这一图像，就宣示了拓扑半金属中 AHE 的可能根源：波矢空间存在“磁单极”，因此引入大的贝里曲率。

这里 v(k) 是波矢 k空间的群速度、ε为能量、E为电场、Ω 乃贝里曲率。可以看到，贝里曲率就是波矢空间的等效磁场。

图 2. (A) 磁性外尔半金属中外尔点对作为一对“磁单极”而激发类似点电荷场一般的贝里曲率，即波矢空间中的等效磁场。这里列举了一系列磁性外尔半金属材料的反常霍尔效应强弱，可以看到 Co₃Sn₂S₂展示了巨大的 AHE，令人惊奇。(B) 波矢空间中一对外尔点及其周围的贝里曲率分布，就像电荷的电力线一般，形成磁单极等效磁场。

(A) https://www.cpfs.mpg.de/3197201/Anomalous-Transport-in-Magnetic-Weyl-Semimetal

(B) H. Li et al, Negative magnetoresistance in Diracsemimetal Cd3As2, NC 7, 10301 (2016),https://www.nature.com/articles/ncomms10301

的确，梳理出这一物理图像之后，物理人的视线似乎就被提升到了一个新的高度：(i) AHE 的量子本源是波矢空间的等效磁场。波矢空间的外尔点“磁单极”是等效磁场的源泉，虽然磁单极对数目未必越多就对 AHE 越好。(ii) 具有空间反演对称破缺的外尔半金属，如 TaAs，它满足时间反演对称性，因此不存在 AHE。(iii) 具有时间反演对称破缺的磁性外尔半金属体系，如 Co₃Sn₂S₂，它打破了时间反演对称性，当然必定有 AHE，甚至可能有 giant AHE。因此，如果将眼光暂且拉回到外尔半金属体系，则什么样的外尔半金属可以具有最大的 AHE，就成为一个有价值的问题，值得量子材料人在其中废寝忘食。

来自米国莱斯大学 (Rice university，大米大学) 的华人知名物理学者戴鹏程教授及其团队，与华盛顿大学 (西雅图) 物理系的 Jiun-Haw Chu 教授、橡树岭国家实验室中子散射高人叶峰 (Feng Ye) 博士、法国 UniversiteParis-Saclay 的 Philippe Bourges 博士 (量子材料研究活跃人物) 和位于 Grenoble 的 InstitutLaue-Langevin 合作团队一起，似乎关注到这一课题，并针对磁性拓扑半金属 Co₃Sn_2-xIn_xS₂，开展了卓有成效的研究工作。他们最近将结果整理成文，刊登在《npj QM》上，得到同行的高度关注。图3 所示乃其实验结果之一部分。

Ising 学习一番、整理出几段读书笔记之后，从中能够感受到少许他们的动机和思考。

戴老师是中子散射中人，他的团队选择磁性外尔半金属作为对象，合情合理。而且，选择时间反演对称破缺的磁性体系而不是 TaAs 等非磁性体系，似乎还有更多的物理缘由：(1) 非磁性和磁性外尔半金属都有成对外尔点，但布里渊区中成对外尔点的分布与密度不同。在这一层面上，它们各自的能带特征和霍尔效应就有显著区别，探索磁性外尔半金属的 AHE 其意不可谓不彰。(2) 磁性体系存在额外磁矩，必定会对 AHE 产生额外贡献，需要考虑。或者说，磁结构对外尔半金属 AHE 的影响尚是未尽理解的课题。更进一步，借助诸如掺杂和替代等方式去改变磁结构，也会影响 AHE。而这种影响，将给仅仅基于外尔点“磁单极”的简单物理带来额外复杂性，需要有深刻认知。

图 3. 戴鹏程老师他们针对 kagome 点阵化合物 Co₃Sn_2-xIn_xS₂(x = 0.0 ~ 1.0) 的晶体结构、磁结构、磁性行为和面内反常霍尔电导的实验结果，特别是中子散射解构磁性的结果。可以看到，在面内呈现非共线反铁磁 AFM 序时，已经巨大的霍尔电导又得到显著增强，霍尔电导在 x = 0.15 处增大了几乎一倍或更多。

事实上，前人对那著名的 kagome 点阵化合物 Co₃Sn₂S₂所开展的探索，已经将相关复杂性部分展现出来。对 Co₃Sn₂S₂，Co 自旋取 c 轴方向的铁磁序 (居里温度 T_C = 177K)。探索结果显示，虽然体系呈现 c 轴铁磁态，但 ab 面内 AHE 的贡献，主要来自外尔点“磁单极”带来的贝里曲率贡献，与铁磁性关系不大。这一结果出乎意外，磁性竟然对 AHE 贡献不大？！要知道，在经典磁学图像中，磁性应该是 AHE 的贡献主体。更进一步，如果设定磁结构含有面内反铁磁序，则此类 kagome 点阵的非共线反铁磁 AFM 结构将引入额外的内生磁场、贝里曲率，因此会引入额外的 AHE 贡献。这一物理，正好给探索磁性影响 AHE 提供了一个潜在的机会。

戴鹏程老师他们挑选的体系，正是拓扑半金属 Co₃Sn_2-xIn_xS₂(x = 0.0 ~ 1.0)。基于前人工作的启示，他们也观察到，Sn 与 In 间的替代，在 x 较低时，能够改变晶格中 Co 自旋的取向和晶体磁结构，但外尔半金属特征却得以大致保持。因此，对这一替代体系开展观测，是研究磁结构如何影响 AHE 的良好对象。话说“研究对象选好了，就成功了 90 %”，还是很到位的说辞。戴老师他们的选择阐明了这一到位：的确，Co₃Sn₂S₂(x = 0.0) 呈现 c 轴铁磁性；当 In 替代 Sn 到 x = 0.12 时，体系展示出 c 轴倾斜的面内反铁磁 (c-axis cantedin-plane AFM order)，且 AFM 有序化温度为 90 K；当 x = 0.30 时，c 轴磁矩继续减小，体系趋向面内 kagome 点阵 AFM 序。X 继续增加，面内 AFM 序被不断压制。

很显然，这一替代，给呈现 Co 自旋磁结构演化影响 AHE 带来了机会；也让浸淫中子散射多年的戴鹏程他们，能够构建磁性与 AHE 之间的内在联系。

行文至此，戴老师他们研究的价值和意义已然初步展现出来。结果也的确显示，对不同 x 样品的中子散射与 AHE 测量结果一一对应，证明在 x 位于 0.1 ~ 0.3 范围内时，AHE 磁结构会演化到面内 AFM 序与面外弱铁磁共存，而此时 AHE 达到最大 (最大值出现在 x = 0.15 处)。戴老师他们在论文中展示了详细的结果，感兴趣的读者可以前往阅读文章详细内容。

在 Ising 看来，这是一项物理图像美轮美奂、研究思路和手法直截了当的工作。文章读起来没有太多难度，但展示了 AHE 多重物理根源的实验证据。如果一定要去与 Ising 开篇所杜撰的研究意义挂钩，量子材料人也许可以从中得到启示：磁性外尔半金属“磁单极”携带的贝里曲率，是贡献 AHE 的重要物理。但是，此类 kagome 晶格的非共线反铁磁结构，也可以贡献额外的贝里曲率，也可以对 AHE 产生重要贡献。因此，获取 giant AHE 并非只有一条道，而可能是殊途同归、罗马不遥。

转载内容仅代表作者观点

不代表中科院半导体所立场

编辑：时生