
文章来源:量子材料QuantumMaterials
原文作者:Ising
凝聚态的高地是量子凝聚态,而凝聚态物理的难度高地,当然也在量子凝聚态物理这里。从固体周期结构中电子传播的薛定谔方程开始,到布洛赫定理,再到高阶微扰进入,理解问题的难度即呈现指数上升。条陈而序,列举如下:
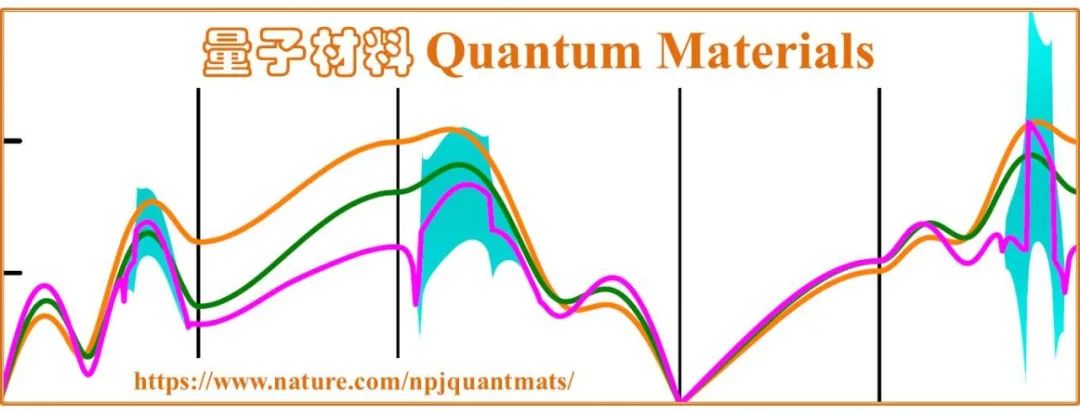
(1) 无论薛定谔方程怎么优美高雅,系统能量 E 就是两大项:动能项 K 和势能项 V:E = K + V,类比于力学系统哈密顿表述。动能项含有动量和有效质量;而势能项,从周期结构出发有 V(x) = V(x + R),其中R是晶格周期矢量。简单的薛定谔方程如图 1(A) 所示。
(2) 电子传输即波动传播。在周期结构中,电子总是勉力前行,力求最大限度地轻便快捷。因此,动能项志在追求更高、更快、更强。物理人可以去找那些迁移率高、有效质量小的体系,特别是那些布里渊区能带变化剧烈而又线性色散的体系。载流子有效质量和飘逸速率的定义如图 1(B) 所示。石墨烯就是范例,动能项强悍、导电性超好。当然,有色散,就有散射、就有电阻损耗。如果能够让所有载流子都步调一致、协同而动,那就是固体输运的极致。所谓超导电性,在电子输运这一层面上理解,大概就是这个意思。现在理解的常规超导,就是所有载流子两两结对,成为玻色子,并凝聚到同一能量处 (玻色统计),从而实现步调一致的、宏观 coherent、无能耗波动!超导电性,就是在动能项中做文章的极致。除此之外,一般的金属,便是有好的导电性,那也是有百利而只一弊:太强的动能项,会掩盖所有弱者,使得纯粹的金属导电在凝聚态物理中有些索然无味!
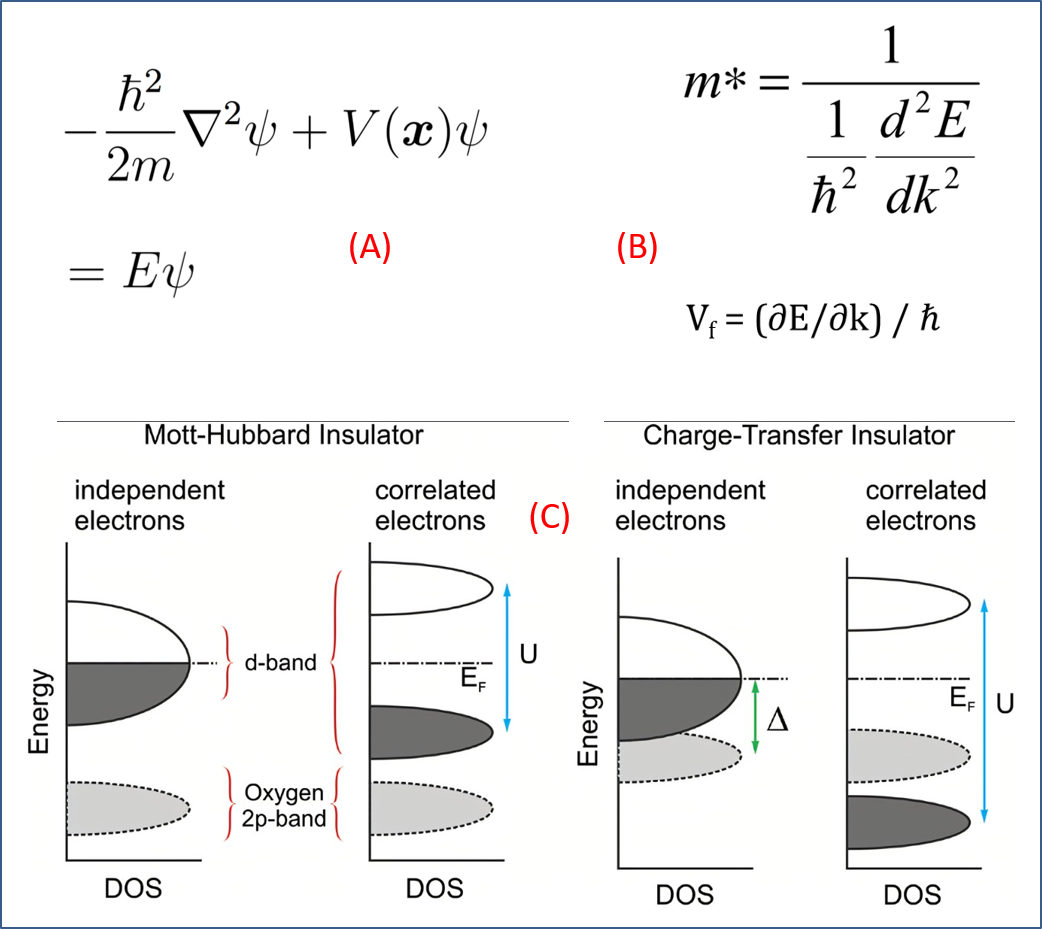
图 1. 固体中电子运动的一些初步知识。(A) 周期结构中的薛定谔波动方程 E,第一项是动能项 K,第二项是势能项 V(x),ψ 是波函数,波矢为 k,E是体系总能量。(B) 载流子有效质量 m* 的定义和漂移速率 Vf 的定义。很显然,如果载流子运动满足线性色散关系,则在费米面交叉点附近的载流子有效质量会很小。漂移速度,因为线性色散会变得很大。(C) 各种相互作用参与到方程的势能项 V(x) 中,会使得费米面附近的能带不断分裂,等效于费米面附近的能带被不断 flatting,即平带化。这些能带的带宽很窄,电子关联、磁性、SOC 等物理进入后,体系就成为展示量子材料风花雪月的舞台。这里展示的是所谓 Mott 绝缘体 (Mott insulator) 和电荷转移绝缘体 (charge-transfer insulator) 两类体系的能带大致样子。可以看到,费米面 Ef 附近能带不断被劈裂,形成若干带宽很窄的子带。
https://251news.com/materials-science-and-engineering/latest-research-on-schrodinger-equation-oct-2019/
https://www.nature.com/articles/am201329
(3) 电子输运,既然是波动,周期性越好,波动就越轻灵顺当。晶格周期性提供的周期势能项,乃为载流子“凌波微步”而天生。但如果破坏了长程周期性 (不是局域于一两个缺陷),一切就都要变脸了。当然,那些叠加到周期性上的畸变涨落,如果能量尺度小、畸变微弱,自然影响不大,无非就是常看到的那些 bad metals。但是,我们议论的问题,正从更高、更快、更强,向更低、更慢、更乱而变化。这里的世界,从物理丰度上评估,要缤纷多彩。打乱长程周期性,使得 V(x) ≠ V(x + R),就可以不那么困难地将动能项 K 压制下去。长程周期性被打乱得越厉害,就越有可能将动能项 K 压制到所剩无几。这似乎就是安德森局域化的最低级科普,也是所谓布里渊区中平带效应起源的最低级科普:平带,意味着没有色散,电子运动就没有了驱动力。图 1(C) 所示即是平带化的能带形态。
(4) 既然 K 变得很小,而 V 又叠加了各种非周期性,那些对载流子周期性波动影响较小的能量项就凸显出来,成为物理研究的渊源。破坏这种周期性的物理很多,如电子库伦关联 U、磁性 S、自旋-轨道耦合 SOC 等,都曾经是、并依旧是量子凝聚态研究的核心和前沿。其中,电子关联能量 U,可能比其它几个因素的影响更大,因此也优先成为量子凝聚态研究的对象。特别是在高温超导物理之后,电子关联物理更是备受关切。当然,个中问题复杂、解决之路漫长,姑且在此不论。总之,压制电子波动动能,乃通过打乱势能周期性、增加阻力、避开强者而实现,也终于可以让那些弱者“当家作主”了一回。
如上四项条陈,如果不全是妄言,则量子凝聚态物理低级科普版大概就是这样了。曾经的研究前沿,很多都是这两大项此消彼长、你方唱罢我登场的阵势。或者说,我们追逐的那些凝聚态体系,要么“能高而规整”、要么“能低而关联”。特别是后者,具有蔚为壮观的新风景。拓扑量子凝聚态进来后,此中局面有所改变。但是,因为对称性、电荷自由度和能带结构于拓扑量子物理中的巨大重要性,这四项条陈依然有效!
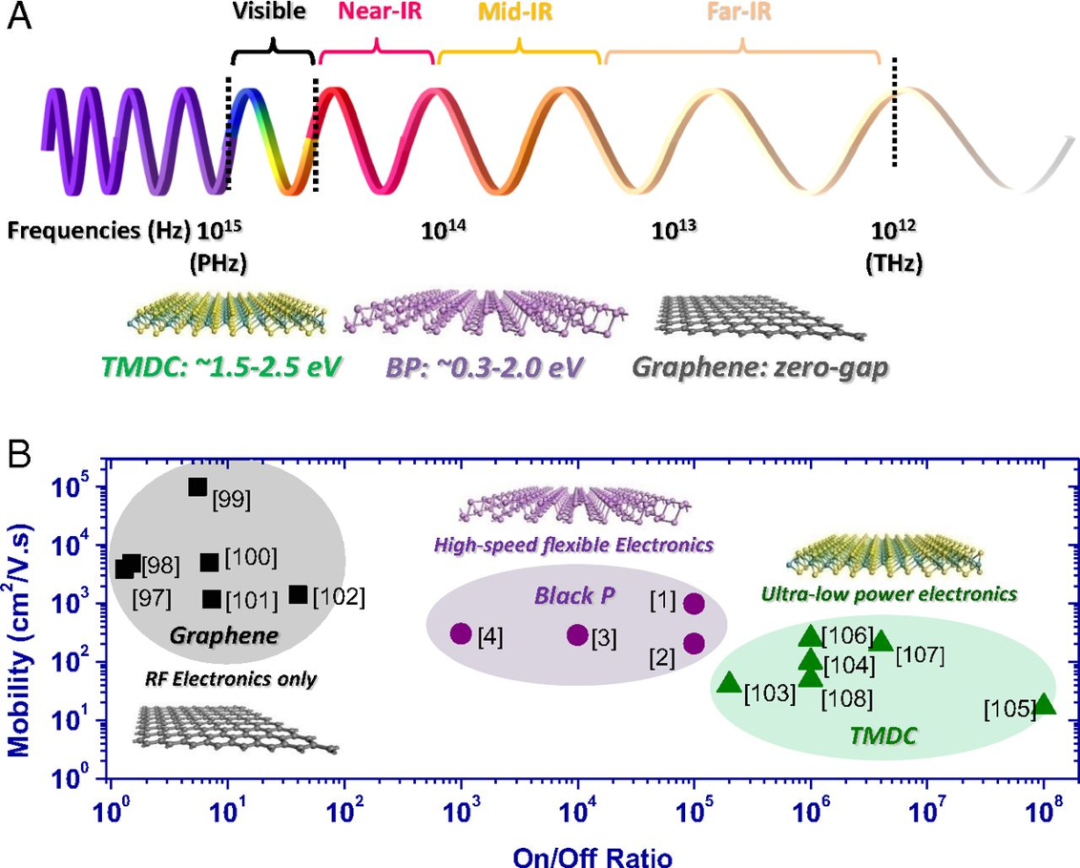
图 2. 一些二维 vdW 材料的典型性能。图中所示内涵清晰,无需注解。图中 [** ] 内数字是来源文章中列出的参考文献序号。
X. Ling et al, PNAS 112, 4523 (2015),https://www.pnas.org/doi/full/10.1073/pnas.1416581112
问题是,人类的追逐没有止境:能否此长彼亦长、同台而交歌呢。那些具有线性色散的金属或窄带半导体,有无可能让电子关联、磁性、SOC 等也同台演出?若此,岂不是《今夜无人入睡》?这样的追逐,就是当前量子凝聚态的前沿。沿这一思路,不妨看一个具体体系 —— 位居二维材料之首的石墨烯。石墨烯可能是目前为止所知性能最好的金属体系之一,其狄拉克半金属特征、超高迁移率和几近完美的蜂窝晶格结构,给石墨烯作为万金油以科学支撑。不过,看碳元素 C 的外层电子就知道,这个体系没有强关联、没有磁性、SOC 也弱。即便是将单层石墨烯的高迁移率和半金属特征用到极致,大概也就是一个高性能导电材料 (基于量子输运角度)。因此,物理人很早就将触角延伸到其它二维 vdW 材料,特别是过渡金属硫族化合物 (transition metaldichalcogenides, TMDs),其典型体系和性能如图 2 所示。
当然,自从石墨烯诞生第一天起,那些天才材料人就在盯住这些个不足:没有磁性就掺杂磁性,没有能隙就通过掺杂或引入边缘态产生能隙 (为何要产生能隙不用再说吧),没有拓扑就引入对称性破缺产生非平庸拓扑。如此等等,无一不在这些材料人的追逐之中。石墨烯诞生十多年后,MIT 的量子材料人 (包括曹原博士) 还用巧手做出了双层转角石墨烯,更是这种追逐的新貌。之所以这样说,是因为石墨烯纵然有那么高的迁移率和那么好的导电性,但被层间转角形成 moire 条纹后,也架不住晶格周期性严重损坏后的电子关联高调出山。这是典型的“山中无老虎”而“猴子称霸王”的逻辑:双层石墨烯,在一些特定转角即魔角处,出现强平带效应、很强无序化、甚至超导电性。图 3 所示乃其中一些简单物理图像。
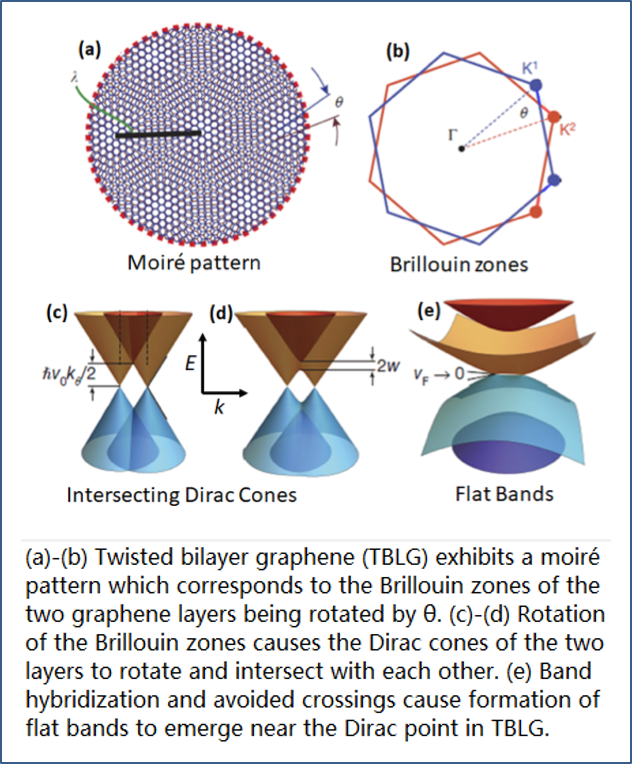
图 3. 蜂窝状石墨烯双层转角形成 moire 形态。两层石墨烯的狄拉克半金属能带,因为转角发生相对偏移,形成一个局部的平带区域 (右下)。
https://crommie.berkeley.edu/research/tlbg/
Y. Cao et al, Nature 556, 80 (2018),https://www.nature.com/articles/nature26154
这一脑洞大开的人工调控术,让全世界的凝聚态物理人都跃跃欲试要转一转石墨烯。转过了石墨烯,就很自然去转那些 vdW 二维材料,终于转出了关联、磁性和 SOC 都有的过渡金属化合物双层 moire 条纹相。
横看整个 vdW 材料范畴,大致上有如下热点卖点:
(1) 石墨烯的 SOC 较弱,但多层石墨烯被转角到平带效应很强时,SOC 的作用会显著起来。这一物理到了含重离子的二维 vdW 材料,SOC 效应更显著。如此,只要继续转角压制住动能,则SOC介入的效果就水涨船高。vdW二维转角材料,之所以成为讨论拓扑、超导和 MIT 等物理妥妥的好平台,原因就在这里。例如,最近就有广受关注的 Wignercrystal、条纹相、反常霍尔绝缘体和拓扑超导态等出现在“二维视觉”中。
(2) 有了两层之间的转角堆砌,就开始有人如法炮制,搞三层对称转角和非对称转角的堆砌。以此类推,相关变化可以很多。不过,增强复杂性,无非是将体系起作用的能量尺度进一步压缩,使得可以参与的物理元素就越多,使得物理越丰富。当然,引入过多复杂因素和变化,也意味着效应出现的条件愈加苛刻、维持稳定的临界温度愈低、距离应用可能就愈远^_^。
(3) 有了同质转角二维材料,便会有人想到搭建异质转角二维材料。同质转角,上下层化学组成和晶体结构一样,转角形成 moire 条纹的规整性好、周期不会那么大、无序度也不会那么离奇。而异质转角,如果两层间晶胞参数不同、组成不同,形成转角结构的形态和空间变化会更加丰富。
果然,过去几年,异质转角二维材料的研究开始受人关注。所谓异质,就是将两种不同的二维单层材料堆砌。从实验角度,对同质和异质转角体系,也许制备和测量技术并无特别的难度差别。但是,从解谱角度看,异质转角体系需要更多自由度介入,因此难度更大。处理这些复杂转角体系的理论方法和第一性计算方法,也亟待发展和深化。从这个意义上,理论上超前预测,并对实验测量结果以深刻解读,便激发量子材料理论学者有更高的热情开展探索。
非为结尾作结尾,从最近的文献,包括本文在内,读者能够体会到:用这类 vdW 二维材料去人工搭建新的体系,可控自由度似乎在发散:双层、多层、同质、异质。往外看去,似乎在走向苍穹和风花雪月。这样的物理,前路多有未知,也更有磕绊:那里是不是能量尺度更小了?调控难度更高了?结果的确定性更差了?可观测的效应更弱了?这里没有答案,答案,在那些宛若天才而甘愿付出的量子材料人脑海里!


