
文章来源:光电汇OESHOW
王飞,司徒国海
中国科学院上海光学精密机械研究所
Part.1
引言
人类感知客观世界的信息,有90%来源于视觉[1],而光学成像技术的发展则大大扩展了人类的视觉能力,使之能上观百亿光年之外的天体运行、下察比头发丝直径还小万倍的分子结构。事实上,只要大家看看自己的智能手机,就能意识到光学成像技术与我们工作生活相关的密切程度。计算光学成像是光学成像与最优化算法、人工智能、信息论等多学科交叉研究方向,吸引着越来越多学术和工业界人员的兴趣。但我们在与同行交流的过程中,也发现有不少人认为这是数字图像处理技术。为了澄清这些误解,本文将简单介绍计算光学成像技术的基本概念、内涵和优势。
Part.2
计算光学成像
计算光学成像,顾名思义,是把“计算”融入到光学图像形成过程中任何一个或者多个环节的一类新型的成像技术或系统。光学图像的形成与场景/物体的照明模式、系统的光学传递函数、像感器的采样三个因素息息相关。计算通常以编码的形式体现在这三个环节当中,对系统的物面、光瞳面和像面(或其共轭面)上的光场进行编码调制,形成编码照明、编码孔径、编码像感(图1)。
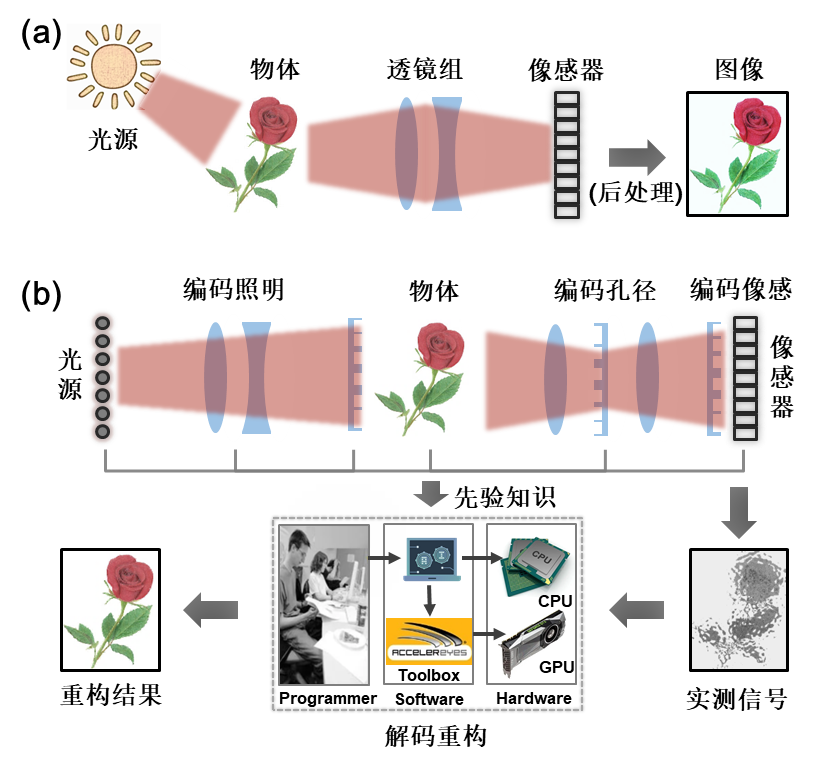
图1. 传统光学成像(a)与计算光学成像(b)的对比示意图
在硬件上,这些编码通常可以专门制作编码板(如微透镜阵列、微偏振片阵列)或者更灵活的可编程控制的空间光调制器(如DMD、LCOS、MEMS、LED阵列),甚至利用光波本身的物理属性(如衍射、相干叠加)来实现;在功能上,编码调制可以作用于光场的光强、相位、偏振、光谱等要素。显然,这些编码器件和函数的引入会导致几何光学意义下光学成像系统“点到点”物像关系不再满足。也即是说,在像感器上所成的像并非“所见即所得”的几何光学像,而是经过“编码”后的光强分布,因而需要用适当的数学算法来“计算重建”场景/物体的图像。因此,计算光学成像系统的设计需要根据具体的成像任务在光学和算法两方面进行联合优化。而数字图像处理技术仅对传统光学成像系统获取到的图像进行后处理(如去噪、像素超分、背景虚化)以获得更好的视觉效果。
Part.3
计算光学成像的技术优势
通过光学与算法的联合优化设计,计算光学成像技术的优势是全方位的(图2)。根据具体的成像任务,计算光学成像技术能扩展成像要素,对光场的相位/传播方向、相空间、偏振态、光谱、时间等参量进行成像;也能提升成像性能,可实现分辨率、视场、景深和动态范围的提升;也能通过去除透镜等方式简化成像系统;甚至在低光照、强散射、存在遮挡物等传统光学成像技术难以应对的环境里,都能获得出色的表现。
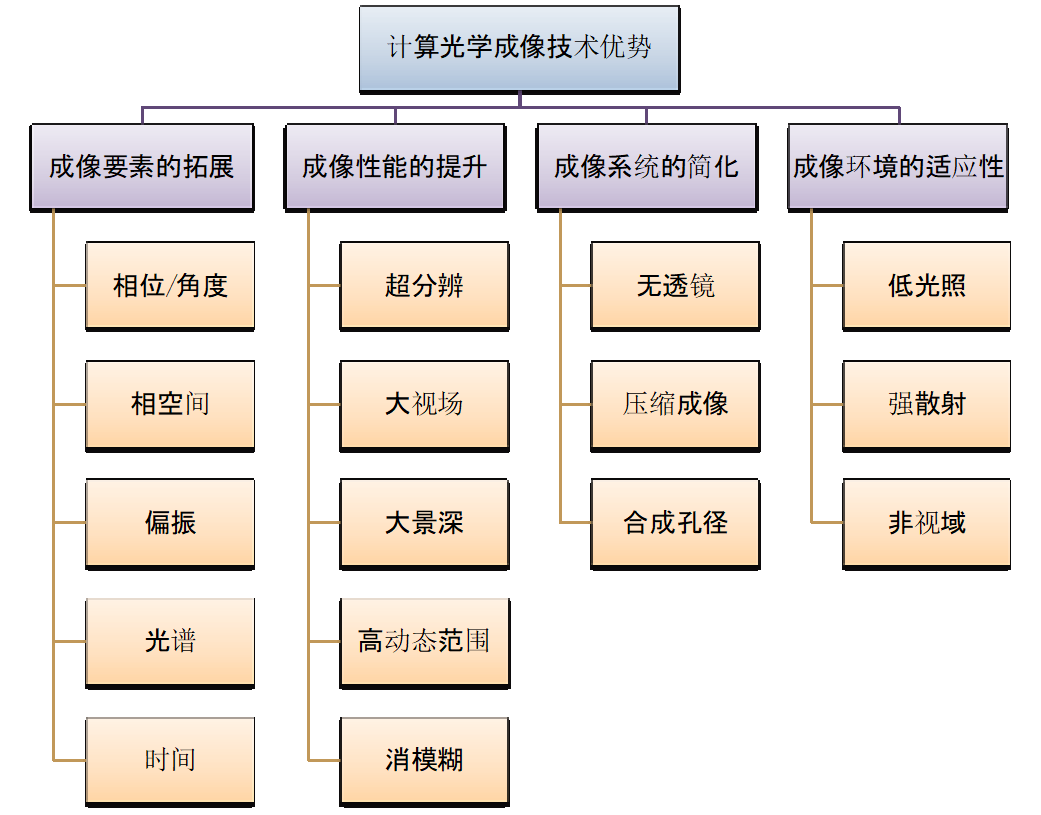
图2. 计算光学成像技术的优势列表
Part.4
计算光学成像中的逆问题及算法
如前所述,因为编码的引入,像感器探测的结果往往不是“所见即所得”的,因而要使用算法从编码探测光强计算重建出物体的图像。实际上,编码探测过程即正向过程可以简单描述为:
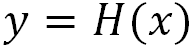
其中,x表示待测物体,H(・)表示整个成像系统的编码探测过程(包含各类噪声),y为实际探测结果。使用算法重构图像即通过逆向过程实现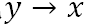 的推理,这是一个典型的逆问题。
的推理,这是一个典型的逆问题。
由于探测过程不可避免的存在信息丢失,上述逆问题往往是病态的,这将导致解的不唯一性,即直接根据y无法唯一确定一个x。
常见的逆问题求解算法可分为以下四类:
1
基于模型的方法
当成像的模型已知时,可以用这类算法来求解。其核心思路是:通过迭代优化的方式,寻找同时满足探测信号约束和物体先验约束的结果。其数学表达式为:
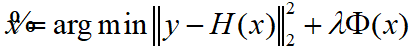
由于逆问题的病态性,满足探测信号约束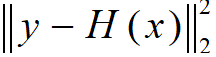 (也称为数据拟合项)的结果有很多,通过手动设计正则项
(也称为数据拟合项)的结果有很多,通过手动设计正则项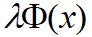 引入诸如稀疏、平滑、支持域等先验约束,可以从众多可行解中挑选“最优解”[2]。最小二乘法、压缩感知算法等都属于此类方法。
引入诸如稀疏、平滑、支持域等先验约束,可以从众多可行解中挑选“最优解”[2]。最小二乘法、压缩感知算法等都属于此类方法。
2
数据驱动方法
当成像的模型难以建立时,可以利用多层神经网络Rθ从大量数据中学习丰富的隐式先验信息,然后利用所得参数模型完成y到x的映射,即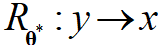 。该方法能够解决传统优化算法无法解决的一些极端环境成像问题(如强散射、极弱光),而且这种方法还是非迭代的,能够实现实时成像[3]。但是,该方法也面临数据获取困难、泛化性及可解释性差等问题。
。该方法能够解决传统优化算法无法解决的一些极端环境成像问题(如强散射、极弱光),而且这种方法还是非迭代的,能够实现实时成像[3]。但是,该方法也面临数据获取困难、泛化性及可解释性差等问题。
3
数据和模型联合驱动的方法
当成像的模型已知时,可将其融入深度学习算法中,从而联合使用物理先验和数据先验。一些联合驱动方法将数据预训练网络作为模型驱动优化算法的正则项,包括基于生成网络引入数据分布先验(仅在该分布下迭代寻优)、基于去噪网络对迭代搜索结果进行约束等;也可直接使用模型对数据预训练网络进行微调,此时网络可快速输出重构结果,若其中出现伪影,再通过模型驱动的方式微调网络参数,兼顾数据驱动方法的时效性和模型驱动优化算法的普适性[4]。这类方法通过协同使用模型与数据,有望解决传统模型驱动与数据驱动方法的瓶颈问题,从而促进计算光学成像技术的实际应用。
4
光学神经网络方法
此前介绍的重构算法都是对数字信号进行处理,而基于光学重构的方法可直接处理模拟信号。该方法首先通过数字计算获得用于处理模拟信号的光学模型(如光神经网络),然后定制加工实体,再将其置于成像系统中处理光信号,从而获得成像结果。这种基于先数字设计再光学处理的方法将图像重构速度提升至光速,且在重构过程不需要使用计算机,具有低功耗的特点[5]。
Part.5
若干典型的计算光学成像技术
下面,我们将列举若干典型的计算光学成像技术。
1
透过散射介质成像
传统成像利用透镜将物点发出的光再次汇聚为像点,然而当成像路径上存在云、雾、烟、尘、霾、生物组织等随机散射介质时,由于光波前因散射而扰乱,传统的光学成像方法难以应对。计算光学成像技术为解决这一难题提供了若干新思路,可以通过波前编码、数字全息、散斑的记忆效应、深度学习等方法实现透过散射介质成像(图3)。
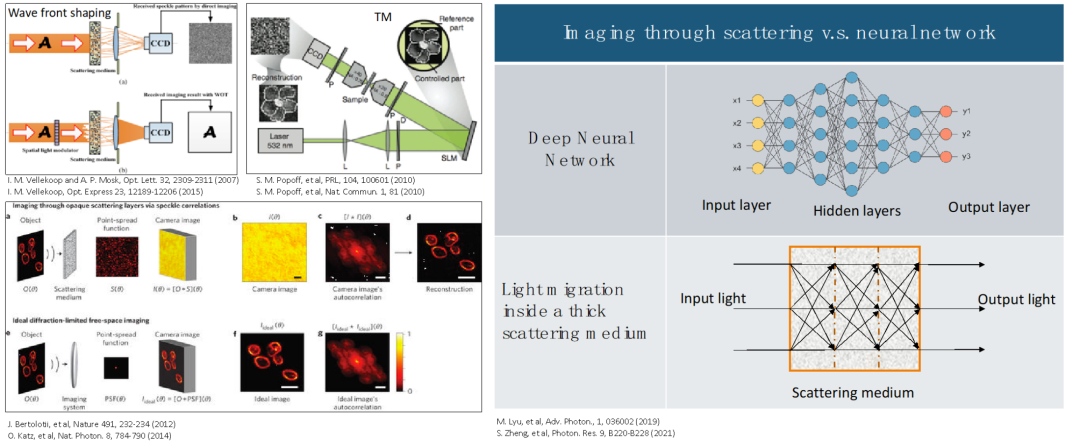
图3.透过散射介质成像的若干典型方法[6]
2
三维成像
我们生活在三维世界中,而传统成像会将场景中不同深度的图像耦合到一幅二维平面图像中,丢失了物体距离观测面的距离即深度信息(图4)。三维成像技术通过设计主动(如结构光照明、激光雷达等)或被动(如双目视觉、编码孔径)的编码方式,使得位于不同深度的物体具有不同的强度响应,从而实现深度信息的获取。该技术在自动驾驶、遥感等领域具有广泛的应用前景。

图4. 二维平面图与深度图[7]
3
多光谱成像
物质在不同波段下的响应能够很好的表征其属性,就像指纹一样。传统彩色相机只能获得几个谱段耦合的图像,因而无法准确获得物质的光谱特征。传统光谱仪需要进行逐点扫描,其信息获取效率受到了极大地限制。光谱成像技术通过棱镜分光和孔径编码,对不同波段的信息进行编码,然后利用重构算法解算不同光谱通道的结构信息,能够通过单次曝光就能实现多谱段图像重建。
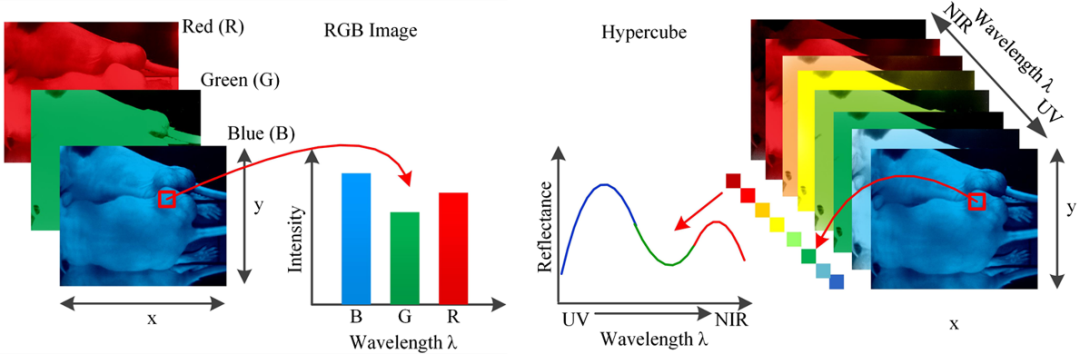
图5. RGB图像与多光谱图像[8]
4
无透镜成像
透镜是传统成像系统中的基本元件,是导致单反相机笨重且昂贵、手机摄像头凸起的“罪魁祸首”。无透镜成像技术通过使用非常规“透镜”(也可直接空间自由传播),如菲涅尔波带片、优化设计的透明薄片等,结合重构算法,实现(逼近)复杂透镜组方能实现的成像效果。该技术能够大幅减少系统的空间体积和重量,对于实现商业产品的轻薄化具有重要意义。

图6. 优化设计的微型透镜与传统透镜[9]
5
单像素成像
传统成像使用千万像素的面阵像感器对光场强度进行采样,此时携带物体信息的光被分到众多像素单元,为保证成像质量,往往需要保证较高的光照度。此外,由于工艺的限制,在一些特殊波段如X-ray、THz,人们难以制备高像素分辨的面阵像感器。单像素成像通过使用DMD、SLM、LED、旋转的毛玻璃等调制器件实现多次二维空间图像信息编码,并使用仅具有单个像素的探测器获得一维时序光强涨落信号,然后利用算法重构获得二维图像。由于所有光子都被一个像素收集且单个像素的探测器容易制备,单像素成像具有探测灵敏度高、适用于特殊波段成像的优势。
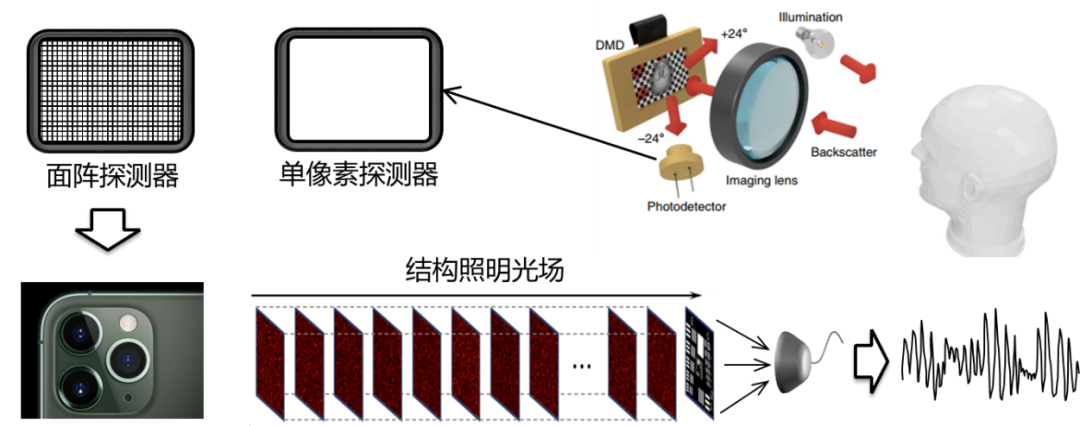
图7. 面阵探测与单像素探测[10]
Part.6
结束语
计算光学成像新机制、新算法、新问题不断涌现,已然成为光学工程领域的一个热门研究方向。国内外从事相关研究的科研工作者越来越多,也正是在整个领域的推动下,该方向正在逐步迈入实用化、智能化的发展阶段。本文仅能如蜻蜓点水般交代其基本概念和内涵,感兴趣的读者可以阅读最近出版的一些中外文献[3, 11,12],以获得对具体的专题更深入的了解。我们也相信在不久的将来,计算光学成像技术将在光信息感知问题中广泛应用,并为科研、医疗、安防、工业、交通等领域带来新的机遇。
参考文献
转载内容仅代表作者观点
不代表中科院半导体所立场
编辑:了之


