来源：大小吴的数学课堂

作者：大小吴

互质（互素），是一个同学们在小学五六年级便熟悉的数学知识内容，它的定义是：若个整数的最大公因数是1，则称这个整数互质.

互质这个概念本身并不难理解.举两个简单的例子，6和12不互质，8和9互质，这是因为

可以发现，判断两数是否互质的基本原理便是将它们分解质因数之后看是否存在相同的质因数.

那么，对于互质，我们是否可以更直观地理解它？为了说明这个问题，首先我们要介绍一种新的方法来记录一个（正）整数.

我们知道，由算术基本定理，任何一个大于1的正整数，若不是质数，则可将其唯一分解成有限个质数的乘积.比如

实际上，我们也可以认为

后面省略的是无穷多的质数，它们的指数都为0，因为显然将40分解质因数之后起作用的质数仅为2和5.

这种记录方法就称为质因数指数记数法，我们甚至可以更简单地将其记为

因为质因数分解的唯一性，所以这个质因数指数记数法和正整数形成了一一对应的关系.也就是说，任何正整数都可以用此方法来表示.

数学家认为，质数是构成数字的“最基本元素”，所以上述记数方法就有点类似于对一个正整数进行光扫描，我们希望通过这种记数方式看清这个正整数的结构.

一般地，任何一个正整数都可以根据质因数指数记数法写成下面这种形式

其中为自然数.

现在你可以思考一下，这种记数法与互质有什么关联呢？

再来考虑文章开头举的例子.对于8和9来说，它们的质因数指数记数形式为

为方便起见，我们同时省略两者从第三项开始的0.

在此，你想到了什么？

<<< 左右滑动见更多 >>>

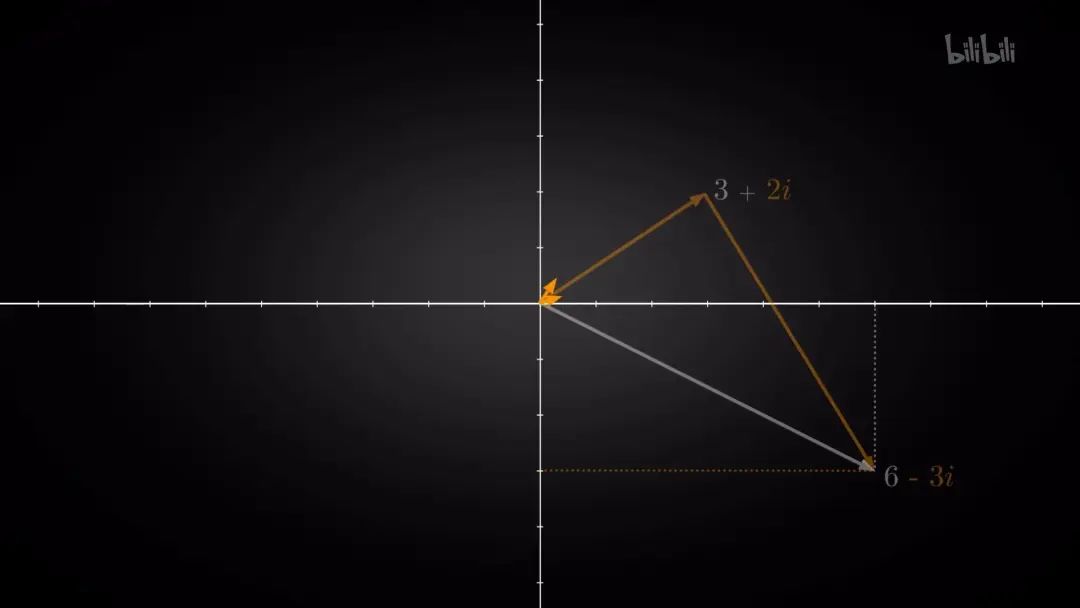
没错，答案就是向量.

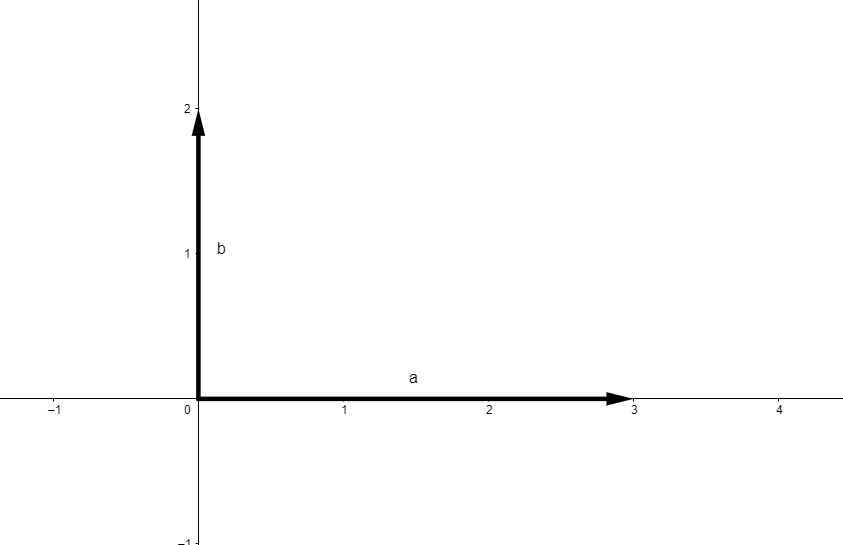
如果将8和9的质因数指数记数形式理解为两个向量

我们便可以很容易理解其几何意义：垂直，或者更专业地说，正交.

为了验证这个猜想，我们再来看一组不互质的例子：

令

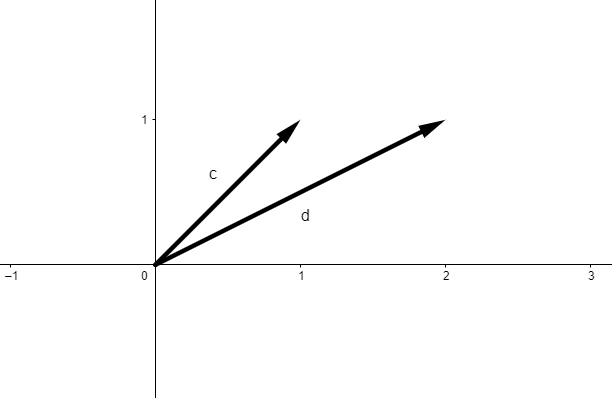
很显然，这里两向量并不垂直.

如果将质因数指数记数法的看成是无限维空间的向量，那么正整数就对应了无限维空间中的一点，便是空间中无数个坐标轴的分量（投影）.把某个正整数分解质因数的过程也即是找寻这个点在各个坐标轴上投影的过程.

因此，两个数“互质”的含义便不难理解了.若两个正整数满足：

互质就等价于最大公因数等于1，而1恰好是

而求最大公因数，即是求质因数指数记数法中各个质数对应分量中较小的那个（然后再重新按指数计算）.

也就是说，互质就意味着对于所有质数，或中肯定有一方为0.从向量角度来说意思就是两个向量不会投影在同一坐标轴上.

我们有如下结论：互质就等价于

参考文献[1]（日）结城浩.数学女孩2:费马大定理[M].丁灵译.人民邮电出版社,2016.

编辑：薛定谔的薛定谔