前言
在Sigma-Delta调制器中，由于运放的增益会随着输出摆幅发生变化，从而积分器输出引起的非线性是一个主要的非理想因素。
为了解决这个问题，有如下思路：
设计高线性度运放，即运放增益随着输出摆幅变化很小，比如避免输出级采用共源共栅，采用Class-AB输出等方法，这在电源电压裕度足够的前提下可以满足线性度要求，但在低压供电下，这种方法变得比较困难； 减小调制器的缩放系数从而使得每一级积分器输出摆幅减小，但会增大积分电容的大小和面积，同时对电路的绝对精度要求变高。(例如同样的一个误差，缩放系数减小会使得它等效到输入误差变大；因此为了避免这种情况，缩放系数减小的同时电路的精度设计也需要提高)。
采用输入前馈结构后，环路只需要处理量化噪声，而不需要处理输入信号，从而减小环路中积分器输出的摆幅，以降低运放引起的非线性。
本文以一个输入前馈结构的二阶Sigma-Delta调制器为例，简单分析了环路中节点的响应，同时通过Matlab代码实现了一个行为级模型，以验证理论分析的正确性。
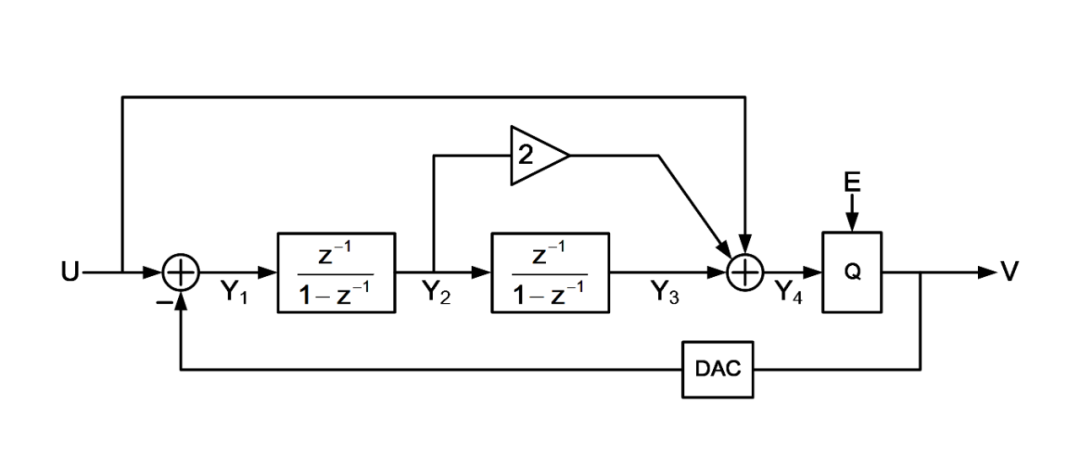图1 二阶输入前馈结构Sigma-Delta调制器
如上图为一个二阶输入前馈结构的Sigma-Delta调制器，其各个节点的响应可以推得：
从式(1)-(5)可知，环路只需要处理量化噪声，即节点Y1，Y2，Y3只是量化噪声的函数，而Y2，Y3为积分器1和积分器2的输出，因此积分器输出摆幅仅受到量化噪声影响，不受到输入信号影响，摆幅被减小。同时，量化器精度越高，量化噪声越小，积分器的摆幅也会越小，调制器的线性度也会越好。
由图1及式(1)-(2)可知，要使得环路只处理量化噪声，即节点Y1不包含输入，则需要输入U到输出V，再经过DAC反馈回来与输入U作减法这一路径没有延迟，换句话说就是要保证DAC反馈的信号中U的分量必须和当前输入U是同一个时刻的值。这就意味着电路实现时，需要在一个时钟周期内完成量化和DAC反馈这个过程，采用多位量化结构还需要同时完成DEM，DWA等，因此对电路实现要求变得更高。在电路设计时，需要精心设计时序满足这一条件，才能完美发挥出输入前馈结构的优点。
本文基于Matlab简单实现了图1所示的二阶输入前馈Sigma-Delta调制器，代码如下：
(注：代码中部分函数来自Delta-Sigma Toolbox，需要安装该工具箱代码才可运行)
clear
format long;
OSR=128;
Nfft=2^16;% fft points
fs=1e6;% sample frequency=1MHz
fbin=17;
fin=fs/Nfft*fbin;% Signal frequency
pi=3.1415926;
w=2*pi*fin;
ts=1/fs;
Vref=1;
% Generate Input signal
Vin_amp=0.7;%0.7 full-scale
fori=1:Nfft+1000
Vin(i)=Vin_amp*sin(w*ts*i);
end
% modulator work
% Vout1 is the output of 1st integrator
% Vout1 is the output of 2nd integrator
Vout1(1)=0;
Vout2(1)=0;
%Extra 100 points
fori=1:Nfft+100
Vsum(i)=Vin(i)+2*Vout1(i)+Vout2(i);
% 4-bit quantizer
bs(i)=0;
forj=1:16
ifVsum(i)>(-17*Vref/16+j*2*Vref/16)
bs(i)=j;
end
end
% Integrator-1 with delay
Vout1(i+1) = Vout1(i)+Vin(i)+(16-2*bs(i))/16*Vref;
% Integrator-2 with delay
Vout2(i+1) = Vout2(i)+Vout1(i);
end
% fft
f=linspace(0,1,Nfft+1);
f=f(1:Nfft);
v=bs(length(bs)-Nfft+1:length(bs));
v=(v-8)/8;% Remove DC and mormalize
V=fft(v.*ds_hann(Nfft))/(Nfft/4);% Hanning window
sig_bins=fbin+[-2:3];
inband_bins=setdiff(1:Nfft/(2*OSR)+1,sig_bins);
SQNR=dbv(norm(V(sig_bins))/norm(V(inband_bins)));
ENOB=(SQNR-1.76)/6.02;
figure(1); clf;
semilogx(f,dbv(V),'b');
grid on;
title ('MOD2-with-Feedforward');
xlabel('Normalized Frequency (f/fs)');
ylabel('PSD (dBFS/NBW)');
text_handle = text(0.005,-20, sprintf('SQNR = %4.1fdB@OSR=%d\n',SQNR,OSR));
text_handle = text(0.005,-35, sprintf('ENOB = %2.2fbits@OSR=%d\n',ENOB,OSR));
figure(2); clf;
edges=[-0.0625,-0.05,-0.0375,-0.0250,-0.0125,0,0.0125,0.0250,0.0375,0.05,0.0625];
histogram(Vout2,edges);
axis([-0.0750.07508000]);
set(gca,'XTick',[-0.0625-0.0375-0.01250.01250.03750.0625]);
set(gca,'YTick',[2000400060008000]);
grid on;
title ('积分器2输出值分布');
xlabel('积分器输出值');
ylabel('数量');
为了让量化噪声足够小以能够清晰地判断出每个积分器的输出是否仅和量化噪声相关，本代码实现的调制器采用了一个4bit量化器。感兴趣的读者可以运行该代码得到SNR等调制器的性能结果，本文不再赘述。
仿真后将积分器2的输出分布绘制得到如下图：
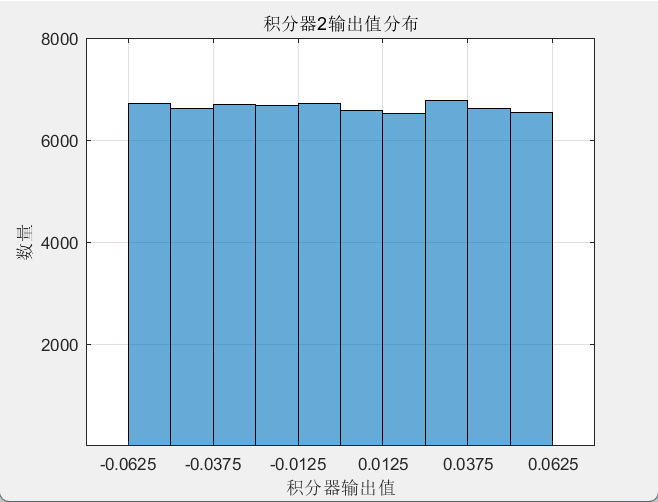
如上图所示，积分器2输出在(-0.625~0.625)之间均匀分布。从式(4)可知，积分器2输出为量化器量化噪声延迟两个时钟周期的值，因此积分器2输出和量化器量化噪声具有相同的电压分布。量化器的量化噪声一般在-Δ/2~Δ/2之间均匀分布，而在本文代码中，量化器满量程为2（即-1~1），量化器为4bit，因此Δ为2/16=0.125，因此量化器的量化噪声应该在-0.625~0.625之间均匀分布，与图2相吻合。因此，这证明了式(4)理论的正确性，也验证了前馈结构环路仅处理量化噪声的结论。
根据式(3)可知，环路中积分器1输出是量化噪声与其他函数的乘积，因此不会像积分器2输出这样均匀分布，虽然如此，由于其仅仅和量化噪声相关，因此幅值很小。（积分器1输出为两个服从图2所示均匀分布的数值之差，感兴趣的读者可以分析其分布情况）
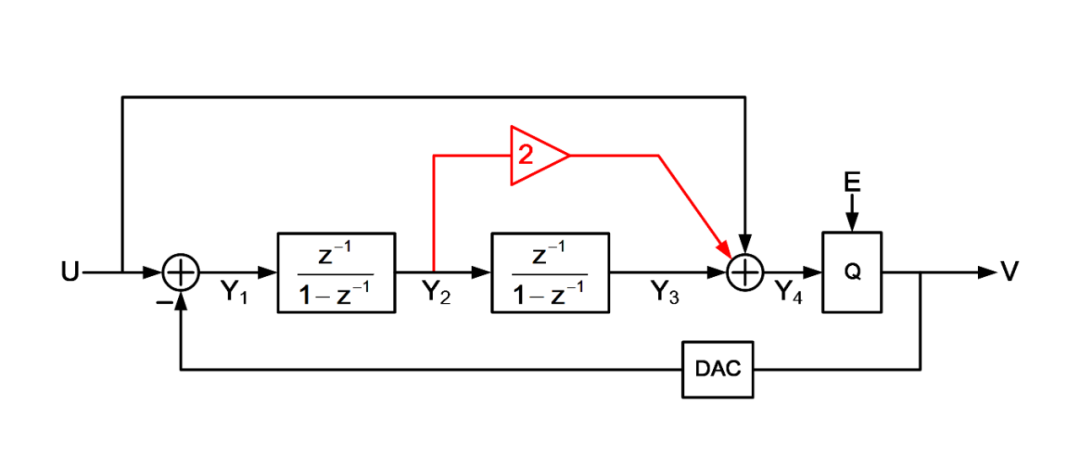
图3 二阶输入前馈结构Sigma-Delta调制器-前馈通路2标红
再回到调制器结构，可以发现除了输入到量化器输入的前馈外，调制器还存在一条从积分器1输出到量化器输入的增益为2的前馈通路，如图3标红部分所示。那这条通路的作用是什么？它是如何被加入环路中的？
基于这个问题，笔者大胆按照自己的理解揣测一下前馈结构初始被设计时的思路，如下所述：
步骤1：设计一个具有二阶噪声整形效果的调制器，不特别设计NTF的零点，即将两个零点都放在DC处，因此NTF设计为：NTF=(1-z-1)2;
步骤2：为了使得环路仅处理量化噪声，引入输入前馈通路，即使STF=1；
步骤3：按照步骤1和步骤2，搭建如图3所示除了标红部分外的其他模块；
步骤4：V=U×STF+E×NTF=U+(1-z-1)2E，因此反推出Y4=V-E=U+(-2z-1+z-2)E;
步骤5：由V可分别推出Y1,Y2,Y3分别为-(1-z-1)2E，-(1-z-1)z-1E和-z-2E；
步骤6：Y4减去输入前馈U，积分器2输出Y3后，还余下-2(1-z-1)z-1E，这刚好是积分器1输出Y2的2倍，因此通过一个增益为2的积分器1输出到量化器输入的前馈路径来补齐该部分。
综上便是笔者关于本文前馈结构调制器由来的一个小小的揣测，感兴趣的读者可以据此对更高阶输入前馈结构进行推理验证。
本文简单介绍了输入前馈结构的Sigma-Delta调制器，以一个二阶输入前馈Sigma-Delta调制器为例分析了其环路关键节点的响应，并通过Matlab行为级模型验证了理论分析的正确性。最后，简单揣测了二阶输入前馈Sigma-Delta调制器的设计思路。希望读者可以通过此文有所收获，不足之处请多多指正。
