真随机数发生器(TRNG)在统计学、信息安全等领域有着广泛的应用。在这些领域中,不仅要求数据序列分布均匀、彼此独立,而且要求其具有不可预测性,能够抵御针对随机性的攻击。B.Sunar,W.J.Martin和D.R.Stinson提出,真随机数发生器的性能受3个因素的影响:熵源(Entropy Source),采集方式(Harvesting Mechanism)和后续处理(Post-Processing)。在电路系统中最常见的三种真随机数产生方法为:1)直接放大法:放大电路中的电阻热噪声等物理噪声,通过比较器进行比较后获得随机数序列;2)振荡采样法:用带有抖动的慢振荡器通过D触发器采样一个周期固定的快振荡器,输出随机序列;3)离散时间混沌法:利用混沌电路不可预测以及对初始条件敏感的依赖性的特点产生随机序列。基于模拟电路的结构,熵源的统计分布更加理想,且熵源噪声不随采样周期的变化而改变;基于数字电路的结构,集成度高,便于在FPGA等通用可编程平台上实现,但熵源的统计特性与模拟电路相比不够理想。
本文引用地址:http://www.eepw.com.cn/article/269579.htm本文尝试了一种用纯数字电路实现的TRNG结构,且不使用诸如PLL等特殊资源,便于设计由FPGA验证移植到芯片设计。其核心思想是使用反相器和延时单元构成两个相互独立的振荡器,由于内部噪声的差异引起的相位偏移作为熵源,经过一段时间振荡后,随机的状态由数字双稳态电路锁存。多组振荡器的输出,经过异或和同步处理后得到随机序列。该TRNG在FPGA物理平台上实现并进行了测试验证。
1 TRNG的设计
1.1 相位漂移与抖动
由于受到电路中噪声的影响,数字电路中时钟信号的周期在每个不同的周期上可能缩短或者加长,这就是时钟抖动。抖动可以用许多方法来衡量和表征,它是一个均值为零的随机变量。振荡器起振时刻的差异和电路元件的工艺偏差,使得振荡器间存在相位漂移。因此抖动信号和相位漂移适合在数字电路中作为TRNG的随机源。
1.2 亚稳态
锁存器是有逻辑‘1’和‘0’两个稳定状态的双稳态器件,但是在特殊情况下其可能进入亚稳态,此时它的输出是介于‘1’和‘0’之间的中间电平。如图1所示锁存器用两个反相器和两个开关表征。当锁存器导通时,采样开关闭合,保持开关打开(图a);当锁存器关闭时,采样开关打开,保持开关闭合(图b)。图c展示了两个反相器的直流传输特性。当锁存器关闭时A=B,稳态是A=B=0和A=B=VDD,亚稳态为A=B= Vm,其中Vm不是一个合理的逻辑值。因为电平在该点是相互稳定的并且可以无限期停留,所以称该点为亚稳态。但是,任何噪声或者其他干扰都会使得A和B最终稳定在两个稳态中的一个状态。图d非常形象地表征了亚稳态,它就好像处于山顶的小球任何干扰都会使小球滚落到山两端的稳定状态。

1.3 振荡器的设计
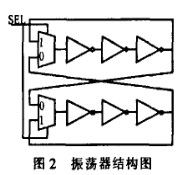
如图2所示,二选一复用器既作为延迟单元又作为选通单元使用。当选通信号为‘1’时,形成两个相互独立、自由振荡的环形振荡器。当选通信号为‘0’时,两组反相器交叉相连形成双稳态器件。自由振荡时,两个振荡器之间存在着抖动和相位偏移。在振荡的停止时刻,即振荡环路断开、两组反相器交叉连接时,反相器的瞬时输出电压以及内部噪声的绝对和相对值决定了电路最终稳定在哪个逻辑值上。有时即使反相器跨接在一起,电路也会振荡很长一段时间才能稳定下来,形成亚稳态。综上所述,随机序列的来源用到了抖动和亚稳态两种机制。
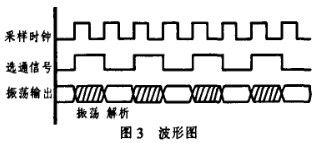
波形如图3所示,为了方便数据采集选通信号是由时钟经过分频得到的。在自由振荡阶段,输出信号快速变化不属于任何稳定状态,在图中用斜线表示。在解析阶段,电路是双稳态器件,此时应该保持解析时间足够长,从而使输出电平在大多数情况下稳定在逻辑‘1’或‘0’。
1.4 随机源模块的电路设计
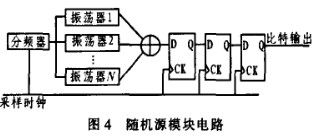
各个振荡器的输出经过异或运算可以增加随机性,而亚稳态的传播会造成后续电路的错误动作,因此使用同步器将异或后的随机序列与后续电路隔离开来,同时也方便采集稳定的输出序列做性能分析。此处采用了三级寄存器的同步结构,由MTBF(Mean Time Between Failure)的定义可知,平均需要经过数百年时间才会发生一次亚稳态通过同步器向下传播的事件,因此是满足设计要求的。该模块电路图如图4所示。
1.5 后续处理模块的设计
理想情况下,D触发器所采集的信号具有随机的统计特性,可是FPGA内部电路不可避免地会受到温度漂移、电压抖动等不良因素影响,从而导致采样得到的随机信号中存在偏置,影响结果的统计特性。所以在采样得到随机序列后要对数据进行消偏处理,使0和1出现的概率相当。
本设计采用16位最大长度二进制伪随机序列(Pseudo Random Binary Sequence)的输出与采样得到的随机序列进行异或运算作为后续处理,PRBS产生电路消耗资源少并且使用线性反馈移位寄存器实现,非常适合于在FPGA上实现。它的生成多项式是:
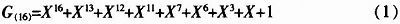
多项式表示如图5所示。


