1 探究背景及试验流程
GB 4943.1-2011《信息技术设备安全第1 部分:通用要求》标准第1.4.12 条款“温度测量条件”中,对相关电气元件的温度限值作出了明确规定:对于非温度依赖型设备相关元件的最高温度(T)不得超过温度限值(Tmax+Tamb-Tma)
从温度限值(Tmax+Tamb-Tma)
笔者为了探究两者间可能存在的某种规律,对随机选取的一系列电源适配器进行温度试验。探究流程如图1。
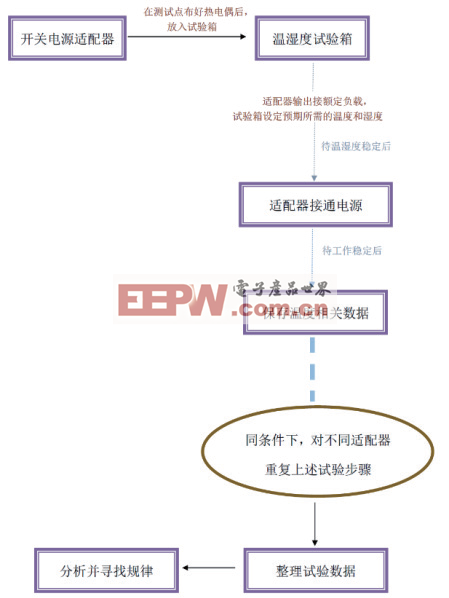
图1 探究流程
2 试验前准备
2.1 选取样品
随机抽取若干开关电源适配器,样品编号及输出规格如下。

2.2 测试环境搭建
测试环境如图2 所示,用一块不透风的布将一个足够大的试验箱(长× 宽× 高=4.5 m×2.1 m×2.7 m)分隔成两个空间,其中开关电源所在空间风速与室内风速相近,约为0~0.2 m/s。
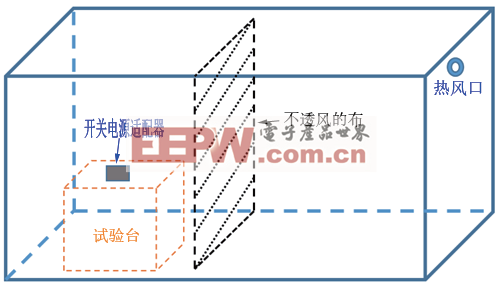
图2 测试环境
2.3 试验方法
试验电压:90 V/50 Hz,264 V/50 Hz;试验箱温度设定:15 ℃开始试验,每隔5 ℃试验一次,依据样品预期的最高环境温度设定试验箱内最高的试验温度;
试验箱湿度设定: 所有试验湿度均设定为55%RH;
输出负载:使用稳定性好的精密电阻作为负载,依据额度输出规格连接对应大小的电阻;当试验箱内温度达到设定值并稳定不少于1 h 后开始接通电源进行试验,待开关电源适配器发热稳定后结束试验。在进行下一轮试验前,开关电源适配器元器件温度需恢复到初始状态。
温度监测点:由于内部元件发热明显,且为了不对内部元件的散热造成太大影响,本探究对内部具有代表性的三个元器件的温度进行监测。三个元器件分别为:初级电解电容、变压器绕组、印制板。
3 试验数据整理及分析
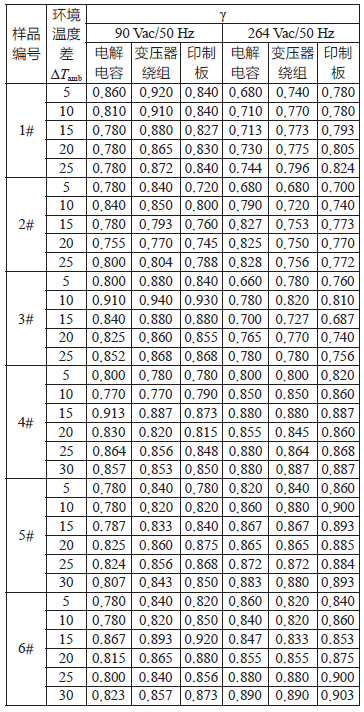
3.1 各样品温度实测值
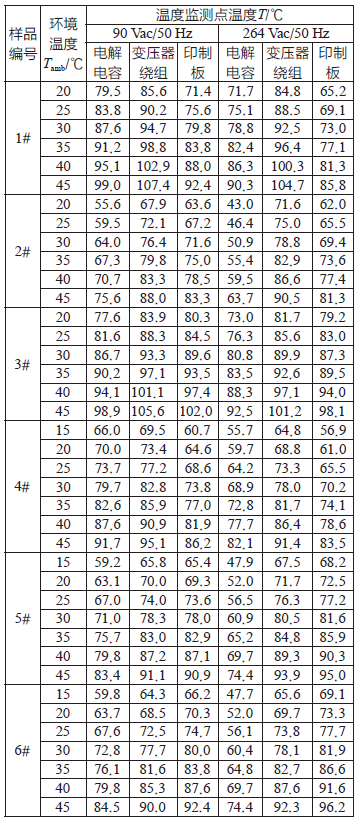
3.2 环境温度差及对应的温度监测点温度差
依据3.1 中的温度数值分别计算环境温度差和温度监测点温度差。
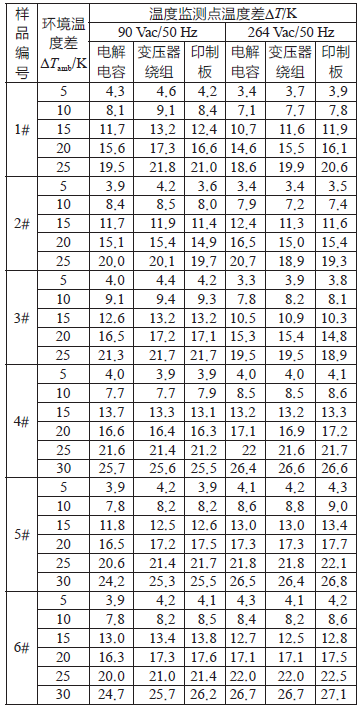
3.3 计算ΔT/ ΔTamb的比值γ
依据3.2 中的数据计算ΔT/ ΔTamb 的比值γ,数值保留3 位有效数字。
3.4 统计分析γ值的规律
从3.3 所得的γ 值可以看出γ 值的分布区间在[0.6,1],且试验电压对γ 值的影响不大。综合统计90 V 和264 V试验电压下不同元器件不同γ 值出现的个数,分别见图3,图4,图5。
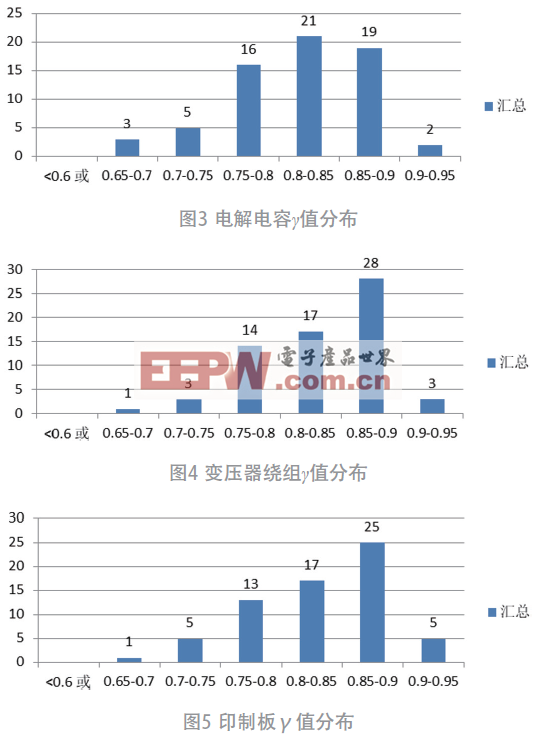
从图3、图4、图5 数据中可以看出不同元件对应的γ 值均主要分布区间为[0.75,0.90]。综合统计所有元器件γ 值共198 组数据,其中分布在[0.75,0.90] 的γ 值有170 组数据,占了总数的85.86%。从统计的数据中分析得出ΔT/ ΔTamb 的比值γ 大概率区间为[0.75,0.90]。
4 结语
经过多组试验的统计处理分析, 当Tamb 升高ΔTamb,经过一段时间元器件发热稳定后,元件的最高温度T 并不是升高ΔTamb,而是小于ΔTamb,且ΔT/ ΔTamb的比值γ 大概率区间为[0.75,0.90]。当Tamb 升高ΔTamb时,应用γ 值去修正元件最高温度即T 升高γ×ΔTamb,再用(T+γ×ΔTamb)与温度限值[Tmax-Tma+(Tamb+ΔTamb)]进行比较。
笔者建议:
1) 若γ=0.75,计算所得的元件最高温度依然超过温度限值,则应要求企业整改;
2) 若γ=0.9,计算所得的元件最高温度小于温度限值但在2 ℃
3) 若γ=0.9,计算所得的元件最高温度小于温度限值且超过2 ℃
在日常的开关电源适配器温升试验中,若常温下试验所得的元器件的最高温度处于温度限值的临界值时,可通过此规律推算出相对准确的试验结果,而不需要花费大量时间和资源成本去重新评估测试,也能有效地解决和回应企业的疑议。如有需要,对于其他电子产品的温升试验结果也可参考上述得出的γ 值,进行相对更准确的判定。
最后,由于试验条件的限制,本论文得出的结论具有一定的局限性,对于监督抽查或类似性质的检测任务,依然需要在符合标准规定的试验条件下开展进一步的试验,以便取得更有说服力的试验结果。
参考文献:
[1] 中华人民共和国国家质量监督检验检疫总局、中国国家标准化管理委员会.GB 4943.1-2011《信息技术设备 安全 第1部分:通用要求》[S].2011.
[2] IEC 60950-1:2005,MOD《Information technology equipment-Safety-Part 1:General requirements》[S].
[3] IEC GUIDE 115(Edition 1.0) 《Application of uncertainty of measurement to conformity assessment activities in the electrotechnical sector》[S].
(本文来源于《电子产品世界》杂志2021年2月期)

